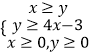题目内容
【题目】已知二次函数![]() .
.
(![]() )若函数
)若函数![]() 在
在![]() 上单调递减,求实数
上单调递减,求实数![]() 的取值范围.
的取值范围.
(![]() )是否存在常数
)是否存在常数![]() ,当
,当![]() 时,
时, ![]() 在值域为区间
在值域为区间![]() 且
且![]() ?
?
【答案】(1) ![]() .(2) 存在常数
.(2) 存在常数![]() ,
, ![]() ,
, ![]() 满足条件.
满足条件.
【解析】试题分析:
(1)结合二次函数的对称轴得到关于实数m的不等式,求解不等式可得实数![]() 的取值范围为
的取值范围为![]() .
.
(2) ![]() 在区间
在区间![]() 上是减函数,在区间
上是减函数,在区间![]() 上是增函数.据此分类讨论:
上是增函数.据此分类讨论:
①当![]() 时,
时, ![]() .
.
②当![]() 时,
时, ![]() .
.
③当![]() ,
, ![]() .
.
综上可知,存在常数![]() ,
, ![]() ,
, ![]() 满足条件.
满足条件.
试题解析:
(![]() )∵二次函数
)∵二次函数![]() 的对称轴为
的对称轴为![]() ,
,
又∵![]() 在
在![]() 上单调递减,
上单调递减,
∴![]() ,
, ![]() ,
,
即实数![]() 的取值范围为
的取值范围为![]() .
.
(![]() )
)![]() 在区间
在区间![]() 上是减函数,在区间
上是减函数,在区间![]() 上是增函数.
上是增函数.
①当![]() 时,在区间
时,在区间![]() 上,
上, ![]() 最大,
最大, ![]() 最小,
最小,
∴![]() ,即
,即![]() ,
,
解得![]() .
.
②当![]() 时,在区间
时,在区间![]() 上,
上, ![]() 最大,
最大, ![]() 最小,
最小,
∴![]() ,解得
,解得![]() .
.
③当![]() ,在区间
,在区间![]() 上,
上, ![]() 最大,
最大, ![]() 最小,
最小,
∴![]() ,即
,即![]() ,
,
解得![]() 或
或![]() ,
,
∴![]() .
.
综上可知,存在常数![]() ,
, ![]() ,
, ![]() 满足条件.
满足条件.

练习册系列答案
相关题目