题目内容
10．
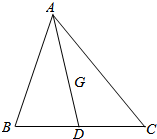如图，AD是△ABC的中线，G是△ABC的重心，设$\overrightarrow{AB}$=$\overrightarrow{a}$，$\overrightarrow{AC}$=$\overrightarrow{b}$，求$\overrightarrow{AD}$、$\overrightarrow{AG}$、$\overrightarrow{DG}$关于$\overrightarrow{a}$、$\overrightarrow{b}$的分解式．
分析 根据向量加法的平行四边形法则便有$\overrightarrow{AD}=\frac{1}{2}（\overrightarrow{a}+\overrightarrow{b}）$，而根据重心的性质有$\overrightarrow{AG}=\frac{2}{3}\overrightarrow{AD}$，$\overrightarrow{DG}=-\frac{1}{3}\overrightarrow{AD}$，这样即可表示出$\overrightarrow{AG}，\overrightarrow{DG}$．
解答 解：根据条件：
$\overrightarrow{AD}=\frac{1}{2}（\overrightarrow{AB}+\overrightarrow{AC}）=\frac{1}{2}（\overrightarrow{a}+\overrightarrow{b}）$，$\overrightarrow{AG}=\frac{2}{3}\overrightarrow{AD}=\frac{1}{3}（\overrightarrow{a}+\overrightarrow{b}）$，$\overrightarrow{DG}=-\frac{1}{3}\overrightarrow{AD}=-\frac{1}{6}（\overrightarrow{a}+\overrightarrow{b}）$．
点评 考查向量加法的平行四边形法则，共线向量基本定理，以及重心的性质：重心到顶点距离是它到对边中点距离的2倍．
练习册系列答案
相关题目
18．若曲线f（x）=x4-2x在点P处的切线垂直于直线x+2y+1=0，则点P的坐标为（ ）
| A． | （1，1） | B． | （1，-1） | C． | （-1，1） | D． | （-1，-1） |
