题目内容
16.若sin2α=$\frac{24}{25}$,则$\sqrt{2}$cos($\frac{π}{4}$-α)的值为±$\frac{7}{5}$.分析 由二倍角的正弦函数公式及同角基本三角函数关系式可求(sinα+cosα)2=$\frac{49}{25}$,利用特殊角的三角函数值及两角差的余弦函数公式即可得解.
解答 解:∵sin2α=2sinαcosα=$\frac{24}{25}$,
∴(sinα+cosα)2=1+2sinαcosα=1+$\frac{24}{25}$=$\frac{49}{25}$,
∴sinα+cosα=±$\frac{7}{5}$,
∴$\sqrt{2}$cos($\frac{π}{4}$-α)=sinα+cosα=±$\frac{7}{5}$.
故答案为:±$\frac{7}{5}$.
点评 本题主要考查了二倍角的正弦函数公式,同角基本三角函数关系式,特殊角的三角函数值及两角差的余弦函数公式的应用,属于基本知识的考查.

练习册系列答案
 高中必刷题系列答案
高中必刷题系列答案
相关题目
5.已知|a|<1,则$\frac{1}{a+1}$与1-a的大小关系为( )
| A. | $\frac{1}{a+1}$<1-a | B. | $\frac{1}{a+1}$>1-a | C. | $\frac{1}{a+1}$≥1-a | D. | $\frac{1}{a+1}$≤1-a |
12.若α,β是一直角三角形两锐角的弧度数,则$\frac{4}{α}$+$\frac{1}{β}$的最小值为( )
| A. | 9 | B. | 18 | C. | $\frac{9}{π}$ | D. | $\frac{18}{π}$ |
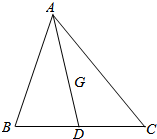 如图,AD是△ABC的中线,G是△ABC的重心,设$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AC}$=$\overrightarrow{b}$,求$\overrightarrow{AD}$、$\overrightarrow{AG}$、$\overrightarrow{DG}$关于$\overrightarrow{a}$、$\overrightarrow{b}$的分解式.
如图,AD是△ABC的中线,G是△ABC的重心,设$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AC}$=$\overrightarrow{b}$,求$\overrightarrow{AD}$、$\overrightarrow{AG}$、$\overrightarrow{DG}$关于$\overrightarrow{a}$、$\overrightarrow{b}$的分解式.