题目内容
19.在△ABC中,设内角A,B,C的对边分别为a,b,c,向量$\overrightarrow{m}$=(cosA,sinA),向量$\overrightarrow{n}$=($\sqrt{2}$-sinA,cosA),若|$\overrightarrow{m}$+$\overrightarrow{n}$|=2.(1)求内角A的大小;
(2)若b=4$\sqrt{2}$,且c=$\sqrt{2}$a,求△ABC的面积.
分析 (1)先求出向量$\overrightarrow{m}+\overrightarrow{n}$的坐标,根据$|\overrightarrow{m}+\overrightarrow{n}|=2$便可得到$\sqrt{4+2\sqrt{2}(cosA-sinA)}=2$,从而可得到cosA=sinA,A是三角形的内角,从而便可得出A的大小为$\frac{π}{4}$;
(2)由余弦定理可建立一个关于a的方程为:${a}^{2}-8\sqrt{2}a+32=0$,这样解出a,从而确定了△ABC的边长,再根据三角形的面积公式即可得出△ABC的面积.
解答 解:(1)$\overrightarrow{m}+\overrightarrow{n}=(\sqrt{2}+cosA-sinA,sinA+cosA)$;
∴$|\overrightarrow{m}+\overrightarrow{n}|=\sqrt{(\sqrt{2}+cosA-sinA)^{2}+(sinA+cosA)^{2}}$=$\sqrt{4+2\sqrt{2}(cosA-sinA)}=2$;
∴$4+2\sqrt{2}(cosA-sinA)=4$;
∴cosA-sinA=0;
∴cosA=sinA;
∵0<A<π;
∴$A=\frac{π}{4}$;
(2)由条件及余弦定理得:
${a}^{2}=(4\sqrt{2})^{2}+(\sqrt{2}a)^{2}-2•4\sqrt{2}•\sqrt{2}a•cos\frac{π}{4}$;
整理得:${a}^{2}-8\sqrt{2}a+32=0$;
解得$a=4\sqrt{2}$;
∴${S}_{△ABC}=\frac{1}{2}•4\sqrt{2}•8•sin\frac{π}{4}=16$.
点评 考查向量坐标的加法运算,根据向量的坐标求向量的长度,cos2A+sin2A=1,以及余弦定理,三角形的面积公式:S=$\frac{1}{2}absinC$.

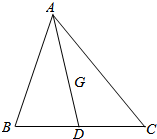 如图,AD是△ABC的中线,G是△ABC的重心,设$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AC}$=$\overrightarrow{b}$,求$\overrightarrow{AD}$、$\overrightarrow{AG}$、$\overrightarrow{DG}$关于$\overrightarrow{a}$、$\overrightarrow{b}$的分解式.
如图,AD是△ABC的中线,G是△ABC的重心,设$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AC}$=$\overrightarrow{b}$,求$\overrightarrow{AD}$、$\overrightarrow{AG}$、$\overrightarrow{DG}$关于$\overrightarrow{a}$、$\overrightarrow{b}$的分解式.