题目内容
2.设公比大于1的正项等比数列{an}满足:a3+a5=20,a2a6=64,则其前6项和为63.分析 由题意可得a3和a5为方程x2-20x+64=0的两根,解方程结合题意可得q=2,a1=1,代入求和公式可得.
解答 解:由等比数列的性质可得a3a5=a2a6=64,
∴a3和a5为方程x2-20x+64=0的两根,
解得a3=4,a5=16,或a3=16,a5=4,
又数列{an}为公比大于1的正项等比数列,
∴a3=4,a5=16,∴q=2,a1=1,
∴其前6项和S6=1−261−2=63
故答案为:63.
点评 本题考查等比数列的求和公式,涉及等比数列的性质和韦达定理,属中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
12.四面体ABCD中,E、F分别为AC、BD中点,若CD=2AB,EF⊥AB,则EF与CD所成的角等于( )
| A. | 30° | B. | 45° | C. | 60° | D. | 90° |
13.函数 f( x)=10x 3-80的零点为( )
| A. | (2,0) | B. | (0,2) | C. | 2 | D. | 0 |
17.执行如图所示的程序框图,则输出的A的值为( )


| A. | 7 | B. | 15 | C. | 29 | D. | 31 |
7.定积分∫e1(1x+2)dx的值为( )
| A. | 2e+1 | B. | 2e-1 | C. | e-2 | D. | 2e-2 |
14.已知f(x)是以2为周期的偶函数,当x∈[0,1]时,f(x)=-x,那么在区间[-1,3]上,关于x的方程f(x)=kx+k-1(其中k为不等于1的实数)有四个不同的实数根,则k的取值范围是( )
| A. | ( ) | B. | (0,12) | C. | (0,14) | D. | (0,13) |
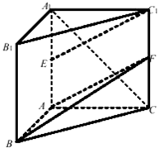 如图,在直三棱柱ABC-A1B1C1中,AB⊥AC,AB=AC=
如图,在直三棱柱ABC-A1B1C1中,AB⊥AC,AB=AC=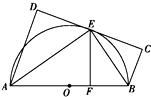 如图,AB为☉O的直径,直线CD与☉O相切于E,AD垂直CD于D,BC垂直CD于C,EF垂直AB于F,连接AE,BE.求证:∠FEB=∠CEB.
如图,AB为☉O的直径,直线CD与☉O相切于E,AD垂直CD于D,BC垂直CD于C,EF垂直AB于F,连接AE,BE.求证:∠FEB=∠CEB.