题目内容
11. 如图,在直三棱柱ABC-A1B1C1中,AB⊥AC,AB=AC=$\frac{\sqrt{2}}{2}A{A}_{1}$,E是棱A1A的中点,F为棱CC1上的一动点.
如图,在直三棱柱ABC-A1B1C1中,AB⊥AC,AB=AC=$\frac{\sqrt{2}}{2}A{A}_{1}$,E是棱A1A的中点,F为棱CC1上的一动点.(Ⅰ)若C1E∥平面ABF,求$\frac{{C}_{1}F}{{C}_{1}C}$的值;
(Ⅱ)在(Ⅰ)的条件下,求证:A1C⊥平面ABF.
分析 (Ⅰ)由题意可得C1E∥FA,又E是棱A1A的中点,可得F为棱CC1的中点,即可得解.
(Ⅱ)由题意可证∠FAC=∠A1CC1,从而可求A1C⊥AF,证明AB⊥平面A1ACC1.即可证明A1C⊥AB,从而得证A1C⊥平面ABF.
解答  解:(Ⅰ)∵C1E∥平面ABF,C1E?平面A1ACC1,
解:(Ⅰ)∵C1E∥平面ABF,C1E?平面A1ACC1,
平面ABF∩平面A1ACC1=AF,
∴C1E∥FA,
∵E是棱A1A的中点,∴F为棱CC1的中点,
∴$\frac{{C}_{1}F}{{C}_{1}C}$=$\frac{1}{2}$;…6分
(Ⅱ)设AB=AC=a,则AA1=$\sqrt{2}a$,
∵$\frac{{A}_{1}{C}_{1}}{{C}_{1}C}=\frac{FC}{AC}=\frac{\sqrt{2}}{2}$,
∴∠FAC=∠A1CC1,
∵∠A1CC1+∠A1CA=90°,∴∠FAC+∠A1CA=90°,
∴A1C⊥AF,
∵A1A⊥平面ABC,AB?平面ABC,∴A1A⊥AB,
∵AB⊥AC,
∴AB⊥平面A1ACC1.
∵A1C?平面A1ACC1,∴AB⊥A1C.
∴A1C⊥AB,A1C⊥AF,
∴A1C⊥平面ABF.…13分.
点评 本题主要考查了直线与平面垂直的判定,直线与平面平行的判定,考查了空间想象能力和推理论证能力,属于中档题.

练习册系列答案
相关题目
19.复数z=$\frac{2-i}{1+i}$(其中i是虚数单位),则z的共轭复数$\overline{z}$=( )
| A. | $\frac{1}{2}$-$\frac{3}{2}$i | B. | -$\frac{1}{2}$-$\frac{3}{2}$i | C. | $\frac{1}{2}$+$\frac{3}{2}$i | D. | -$\frac{1}{2}$+$\frac{3}{2}$i |
6.已知F1,F2分别是中心在坐标原点,对称轴为做标轴的双曲线C的左、右焦点,过F2的直线l与双曲线的右支交于A,B两点,I1,I2分别为△AF1F2,△BF1F2的内心,若双曲线C的离心率为2,|I1I2|=$\frac{9}{2}$,直线l的倾斜角的正弦值为$\frac{8}{9}$,则双曲线C的方程为( )
| A. | x${\;}^{2}+\frac{{y}^{2}}{3}$=1 | B. | $\frac{{x}^{2}}{16}-\frac{{y}^{2}}{48}$=1 | C. | $\frac{{x}^{2}}{2}-\frac{{y}^{2}}{6}$=1 | D. | $\frac{{x}^{2}}{4}$-$\frac{{y}^{2}}{12}$=1 |
16.如图框内的输出结果是( )
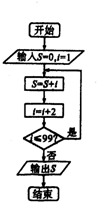

| A. | 2401 | B. | 2500 | C. | 2601 | D. | 2704 |
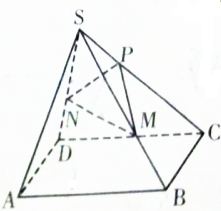 如图,四边形ABCD是正方形,S为四边形ABCD所在平面外一点,SA=SB=SC=SD,P,M,N分别是SC,SB,SD上的点,且PC:SP=SM:MB=SN:ND=2:1,求证:SA∥平面PMN.
如图,四边形ABCD是正方形,S为四边形ABCD所在平面外一点,SA=SB=SC=SD,P,M,N分别是SC,SB,SD上的点,且PC:SP=SM:MB=SN:ND=2:1,求证:SA∥平面PMN.