题目内容
已知点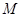 为等边三角形
为等边三角形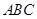 的中心,
的中心,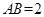 ,直线
,直线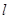 过点
过点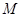 交边
交边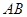 于点
于点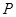 ,交边
,交边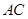 于点
于点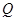 ,则
,则 的最大值为 .
的最大值为 .
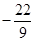
解析试题分析:以M点为原点,x轴平行于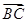 ,y轴垂直于
,y轴垂直于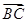 ,建立直角坐标系,则M(0,0),A(0,
,建立直角坐标系,则M(0,0),A(0,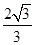 ),B(-1,-
),B(-1,-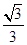 ),C(1,-
),C(1,-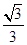 ),设直线l的方程为y="kx" (0≤k≤
),设直线l的方程为y="kx" (0≤k≤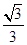 )(1), 直线AB的方程y-
)(1), 直线AB的方程y-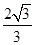 =
=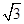 x
x
(2),联立(1)(2),得P点的坐标为(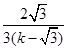 ,
,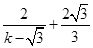 ),
),
直线AC的方程:y-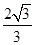 =-
=-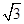 x, (3),
x, (3),
联立(1)(3),得Q点的坐标为(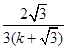 ,
,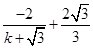 ),
),
则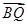 =(
=(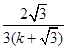 +1,
+1,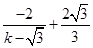 +
+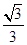 ),即
),即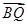 =(
=(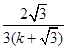 +1,
+1,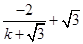 )
)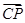 =(
=(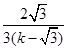 -1,
-1,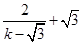 ),
), 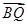 ·
·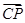 =(
=(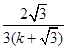 +1)(
+1)(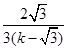 -1)+(
-1)+(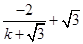 )(
)(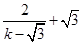 )=
)=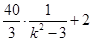 ,
,
因为0≤k≤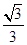 ,
,
所以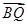 ·
·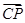 =
=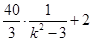 ≤
≤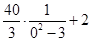 =
=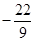 ,当且仅当k=0,即直线l平行于x轴时取等号.
,当且仅当k=0,即直线l平行于x轴时取等号.
故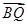 ·
·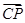 的最大值是
的最大值是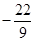 .
.
考点:1.向量的运算;2.直线方程.

练习册系列答案
相关题目
 满足
满足 ,则函数
,则函数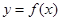 的表达式为 .
的表达式为 . 的模为1,且
的模为1,且 满足
满足 ,则
,则 在
在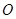 是
是 的三边中垂线的交点,
的三边中垂线的交点,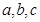 分别为角
分别为角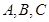 对应的边,已知
对应的边,已知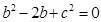 ,则
,则 的范围是_____________.
的范围是_____________.


 中,
中, 分别是
分别是 的中点,
的中点, 为交点,若
为交点,若 =
= ,
, =
= ,
, 、
、 、
、 .
.
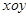 平面上,点
平面上,点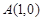 ,点
,点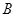 在单位圆上,
在单位圆上,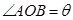 (
(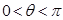 )
)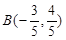 ,求
,求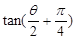 的值;
的值;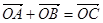 ,四边形
,四边形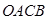 的面积用
的面积用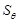 表示,求
表示,求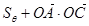 的取值范围.
的取值范围.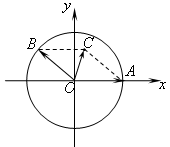
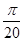 ,求证:a∥b.
,求证:a∥b. 和
和 ,它们的夹角为90°.如图所示,点C在以O为圆心的圆弧
,它们的夹角为90°.如图所示,点C在以O为圆心的圆弧 上运动,若
上运动,若 =x
=x
 =-2i+mj,
=-2i+mj, =ni+j,
=ni+j, =5i-j,若点A、B、C在同一条直线上,且m=2n,求实数m、n的值.
=5i-j,若点A、B、C在同一条直线上,且m=2n,求实数m、n的值.