题目内容
设函数 在定义域内可导,
在定义域内可导,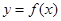 的图像如右图,则导函数
的图像如右图,则导函数 的图像可能是( )
的图像可能是( )
 在定义域内可导,
在定义域内可导,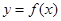 的图像如右图,则导函数
的图像如右图,则导函数 的图像可能是( )
的图像可能是( )
C
试题分析:从
 的图像可以看出,
的图像可以看出, 在
在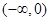 单调递增,所以此时
单调递增,所以此时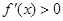 ,可排除A、D,而当
,可排除A、D,而当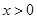 时,
时, 先增后减再增,所以
先增后减再增,所以 在
在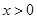 时,是先正后负再正,可排除B,而C则符合要求,故选C.
时,是先正后负再正,可排除B,而C则符合要求,故选C.
练习册系列答案
相关题目
题目内容
 在定义域内可导,
在定义域内可导,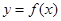 的图像如右图,则导函数
的图像如右图,则导函数 的图像可能是( )
的图像可能是( )
 的图像可以看出,
的图像可以看出, 在
在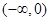 单调递增,所以此时
单调递增,所以此时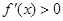 ,可排除A、D,而当
,可排除A、D,而当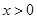 时,
时, 先增后减再增,所以
先增后减再增,所以 在
在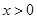 时,是先正后负再正,可排除B,而C则符合要求,故选C.
时,是先正后负再正,可排除B,而C则符合要求,故选C.