题目内容
12.比较1.5-0.2,1.30.7,($\frac{2}{3}$)${\;}^{\frac{1}{3}}$.分析 变形可得($\frac{2}{3}$)${\;}^{\frac{1}{3}}$=$1.{5}^{-\frac{1}{3}}$,由指数函数对的性质可得.
解答 解:变形可得($\frac{2}{3}$)${\;}^{\frac{1}{3}}$=$(\frac{3}{2})^{-\frac{1}{3}}$=$1.{5}^{-\frac{1}{3}}$,
由指数函数y=1.5x在R单调递增可知0<$1.{5}^{-\frac{1}{3}}$<1.5-0.2<1,
同理由指数函数y=1.3x可知1.30.7>1,
∴三个数的大小关系为:$1.{5}^{-\frac{1}{3}}$<1.5-0.2<1.30.7
点评 本题考查指数函数单调性比较数的大小关系,属基础题.

练习册系列答案
相关题目
1.设有一正态总体,它的正态曲线是函数f(x)的图象,且f(x)=$\frac{1}{\sqrt{8π}}$e-$\frac{(x-10)^{2}}{8}$,则这个正态总体的平均数与方差分别是( )
| A. | 10与8 | B. | 10与4 | C. | 8与10 | D. | 4与10 |
2.甲、乙、丙三位学生独立地解同一道题,甲乙做对的概率分别为$\frac{1}{2}$,$\frac{1}{3}$,丙做对的概率为m,且三位学生是否做对相互独立.记ξ为这三位学生中做对该题的人数,其分布列为:
(1)求至少有一位学生做对该题的概率;
(2)求m的值;
(3)求ξ的数学期望.
| ξ | 0 | 1 | 2 | 3 |
| P | $\frac{1}{4}$ | a | b | $\frac{1}{24}$ |
(2)求m的值;
(3)求ξ的数学期望.
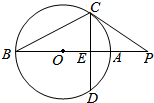 如图,PC切圆O于点C,割线PAB经过圆心O,弦CD⊥AB于点E.
如图,PC切圆O于点C,割线PAB经过圆心O,弦CD⊥AB于点E.