题目内容
20．求y=x（1-x）2（0＜x＜1）的最大值．分析 由题意可得0＜1-x＜1，变形可得y=x（1-x）2=$\frac{1}{2}$•2x•（1-x）（1-x），由基本不等式可得．
解答 解：∵0＜x＜1，∴0＜1-x＜1，
∴y=x（1-x）2=$\frac{1}{2}$•2x•（1-x）（1-x）
≤$\frac{1}{2}$$（\frac{2x+1-x+1-x}{3}）^{3}$=$\frac{4}{27}$
当且仅当2x=1-x即x=$\frac{1}{3}$时取等号，
∴所求最大值为$\frac{4}{27}$
点评 本题考查三次函数的最值，变形利用基本不等式是解决问题的关键，属中档题．
练习册系列答案
相关题目
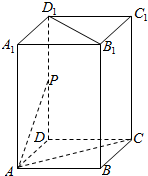如图，在长方体ABCD-A1B1C1D1中，AB=AD=1，AA1=2，点P为DD1的中点．
10．函数f（x）=2-|x+1|的单调递增区间为（ ）
| A． | （-∞，-1） | B． | （-∞，0） | C． | （0，+∞） | D． | （-1，+∞） |