题目内容
2.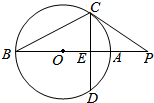 如图,PC切圆O于点C,割线PAB经过圆心O,弦CD⊥AB于点E.
如图,PC切圆O于点C,割线PAB经过圆心O,弦CD⊥AB于点E.(1)求证:PA•PB=PE•PO;
(2)若PC=4,CE=$\frac{12}{5}$,求圆O的面积.
分析 (1)连接OC,则OC⊥PC,利用射影定理,切割线定理,即可证明:PA•PB=PE•PO;
(2)若PC=4,CE=$\frac{12}{5}$,求出PE,可得圆的半径,即可求圆O的面积.
解答 (1)证明:连接OC,则OC⊥PC,
∵CD⊥AB,
∴PC2=PE•PO,
∵PC切圆O于点C,割线PAB经过圆心O,
∴PC2=PA•PB,
∴PA•PB=PE•PO;
(2)解:∵PC=4,CE=$\frac{12}{5}$,
∴PE=$\frac{16}{5}$,
∵PC2=PE•PO,
∴PO=5,
∴OE=$\frac{9}{5}$,
∴OC=3,
∴圆O的面积S=9π.
点评 本题考查射影定理,切割线定理,考查圆的面积,正确运用射影定理,切割线定理是关键.

练习册系列答案
 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案
相关题目
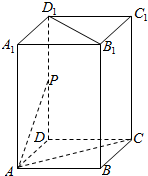 如图,在长方体ABCD-A1B1C1D1中,AB=AD=1,AA1=2,点P为DD1的中点.
如图,在长方体ABCD-A1B1C1D1中,AB=AD=1,AA1=2,点P为DD1的中点.