��Ŀ����
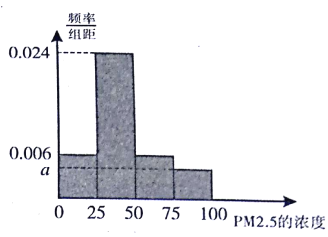
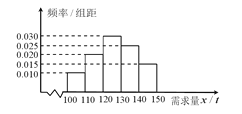
����Ŀ��ij��������һ��������Ԫ�������������������ͼ���ˮƽ�����ƣ������һЩ��Ʒ�����ݾ���֪�������Ʒ��P���ղ���x�������֮����������ϵ�� 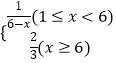 ����ע����Ʒ��=��Ʒ��/����������P=0.1��ʾÿ����10����Ʒ����1��Ϊ��Ʒ������Ϊ�ϸ�Ʒ������֪ÿ����1����ϸ��Ԫ������ӯ��2��Ԫ����ÿ����1�����Ʒ������1��Ԫ���ʳ���ϣ���������ʵ��ղ�����
����ע����Ʒ��=��Ʒ��/����������P=0.1��ʾÿ����10����Ʒ����1��Ϊ��Ʒ������Ϊ�ϸ�Ʒ������֪ÿ����1����ϸ��Ԫ������ӯ��2��Ԫ����ÿ����1�����Ʒ������1��Ԫ���ʳ���ϣ���������ʵ��ղ�����
��1���Խ���������������Ԫ��ÿ���ӯ����T����Ԫ����ʾΪ�ղ���x��������ĺ�����
��2�����ղ���xΪ����ʱ���ɻ���������
���𰸡�
��1���⣺��x��6ʱ��P= ![]() ����T=
����T= ![]() x��2��
x��2�� ![]() x��1=0��
x��1=0��
��1��x��6ʱ��P= ![]() ����T=��1��
����T=��1�� ![]() ��x��2����
��x��2���� ![]() ��x��1=
��x��1= ![]() ��
��
������������ӯ����T����Ԫ�����ղ���x��������ĺ�����ϵΪ��T= 
��2���⣺�ɣ�1��֪����x��6ʱ��ÿ���ӯ��Ϊ0��
��1��x��6ʱ��T��x��= ![]() =15��2[��6��x��+
=15��2[��6��x��+ ![]() ]��15��12=3��
]��15��12=3��
��T��3��
���ҽ���x=3ʱ��T=3��
���ϣ����ղ���Ϊ3���ʱ���ɻ���������3��Ԫ
����������1��ÿ���Ӯ��ΪT=�ղ�����x������Ʒ�ʣ�1��P����2���ղ�����x������Ʒ�ʣ�P����1�����ݷֶκ����ֶ��о����������ɣ���2�����û�������ʽ���������ֵ��

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�