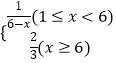题目内容
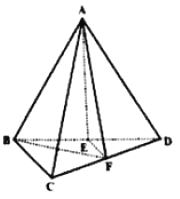
【题目】正四棱锥(底面为正方形,顶点在底面上的射影是底面的中心)S﹣ABCD的底面边长为2,高为2,E为边BC的中点,动点P在表面上运动,并且总保持PE⊥AC,则动点P的轨迹的周长为( )
A.![]()
B.![]()
C.3 ![]()
D.![]()
【答案】D
【解析】解:连接AC,BD交于点O,连接SO,则SO⊥平面ABCD
由AC平面ABCD,故SO⊥AC
取SC中点F和CD中点G,连接GE交AC于H
则H为OC的中点,故FH∥SO,
则FH⊥AC
又由GE∥BD,BD⊥AC得GE⊥AC
∵GE∩FH=H,GE,FH平面FGE
∴AC⊥平面FGE
故当P∈平面FGE时,总有PE⊥AC,
故动点P的轨迹即为△FGE的周长
又∵正四棱锥S﹣ABCD的底面边长为2,高为2,
故SO=2,BD=2 ![]()
则GE= ![]() ,SB=
,SB= ![]()
则FE=FG= ![]()
故△FGE的周长为 ![]()
故选D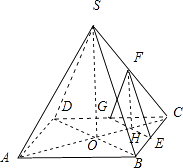
由动点P在正四棱锥的表面上运动,并且总保持PE⊥AC,故P点落在过E点且于AC垂直的平面上,根据线面平行的判定定理,找到满足条件的P点轨迹,解三角形可得答案.

练习册系列答案
 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案
相关题目
【题目】国内某知名连锁店分店开张营业期间,在固定的时间段内消费达到一定标准的顾客可进行一次抽奖活动,随着抽奖活动的有效开展,参与抽奖活动的人数越来越多,该分店经理对开业前![]() 天参加抽奖活动的人数进行统计,
天参加抽奖活动的人数进行统计, ![]() 表示开业第
表示开业第![]() 天参加抽奖活动的人数,得到统计表格如下:
天参加抽奖活动的人数,得到统计表格如下:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
经过进一步统计分析,发现![]() 与
与![]() 具有线性相关关系.
具有线性相关关系.
(1)若从这![]() 天中随机抽取两天,求至少有
天中随机抽取两天,求至少有![]() 天参加抽奖人数超过
天参加抽奖人数超过![]() 的概率;
的概率;
(2)请根据上表提供的数据,用最小二乘法求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ,并估计若该活动持续
,并估计若该活动持续![]() 天,共有多少名顾客参加抽奖.
天,共有多少名顾客参加抽奖.
参考公式: 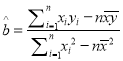 ,
, ![]() .
.