Question

【题目】已知函数f（x）=ex﹣e﹣x﹣2x．
（Ⅰ）讨论f（x）的单调性；
（Ⅱ）设g（x）=f（2x）﹣4bf（x），当x＞0时，g（x）＞0，求b的最大值；
（Ⅲ）已知1.4142＜ ＜1.4143，估计ln2的近似值（精确到0.001）．

Answer 1

【答案】解：（Ⅰ）由f（x）得f′（x）=ex+e﹣x﹣2 ，即f′（x）≥0，当且仅当ex=e﹣x即x=0时，f′（x）=0，
∴函数f（x）在R上为增函数．
（Ⅱ）g（x）=f（2x）﹣4bf（x）=e2x﹣e﹣2x﹣4b（ex﹣e﹣x）+（8b﹣4）x，
则g′（x）=2[e2x+e﹣2x﹣2b（ex+e﹣x）+（4b﹣2）]
=2[（ex+e﹣x）2﹣2b（ex+e﹣x）+（4b﹣4）]
=2（ex+e﹣x﹣2）（ex+e﹣x+2﹣2b）．
①∵ex+e﹣x＞2，ex+e﹣x+2＞4，
∴当2b≤4，即b≤2时，g′（x）≥0，当且仅当x=0时取等号，
从而g（x）在R上为增函数，而g（0）=0，
∴x＞0时，g（x）＞0，符合题意．
②当b＞2时，若x满足2＜ex+e﹣x＜2b﹣2即 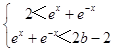，得 ，此时，g′（x）＜0，
又由g（0）=0知，当 时，g（x）＜0，不符合题意．
综合①、②知，b≤2，得b的最大值为2．
（Ⅲ）∵1.4142＜ ＜1.4143，根据（Ⅱ）中g（x）=e2x﹣e﹣2x﹣4b（ex﹣e﹣x）+（8b﹣4）x，
为了凑配ln2，并利用 的近似值，故将ln 即 代入g（x）的解析式中，
得 ．
当b=2时，由g（x）＞0，得 ，
从而 ；
令 ，得 ＞2，当 时，
由g（x）＜0，得 ，得 ．
所以ln2的近似值为0.693
【解析】对第（Ⅰ）问，直接求导后，利用基本不等式可达到目的；
对第（Ⅱ）问，先验证g（0）=0，只需说明g（x）在[0+∞）上为增函数即可，从而问题转化为“判断g′（x）＞0是否成立”的问题；
对第（Ⅲ）问，根据第（Ⅱ）问的结论，设法利用 的近似值，并寻求ln2，于是在b=2及b＞2的情况下分别计算 ，最后可估计ln2的近似值．
【考点精析】关于本题考查的利用导数研究函数的单调性，需要了解一般的,函数的单调性与其导数的正负有如下关系： 在某个区间内，(1)如果，那么函数在这个区间单调递增；(2)如果，那么函数在这个区间单调递减才能得出正确答案．