题目内容
【题目】有次水下考古活动中,潜水员需潜入水深为30米的水底进行作业,其用氧量包含以下三个方面:①下潜时,平均速度为每分钟![]() 米,每分钟的用氧量为
米,每分钟的用氧量为![]() 升;②水底作业需要10分钟,每分钟的用氧量为0.3升;③返回水面时,速度为每分钟
升;②水底作业需要10分钟,每分钟的用氧量为0.3升;③返回水面时,速度为每分钟![]() 米,每分钟用氧量为0.2升;设潜水员在此次考古活动中的总用氧量为
米,每分钟用氧量为0.2升;设潜水员在此次考古活动中的总用氧量为![]() 升;
升;
(1)将![]() 表示为
表示为![]() 的函数;
的函数;
(2)若![]() ,求总用氧量
,求总用氧量![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)
;(2)![]()
【解析】
(1)先由题意,得到下潜所需时间为![]() 分钟,返回所用时间为
分钟,返回所用时间为![]() 分钟,再由题中数据,即可求出结果;
分钟,再由题中数据,即可求出结果;
(2)先由基本不等式求出最小值,再令![]() ,用单调性的定义,判断
,用单调性的定义,判断![]() 在
在![]() 上的单调性,从而可求出最大值,即可得出结果.
上的单调性,从而可求出最大值,即可得出结果.
(1)由题意,下潜所需时间为![]() 分钟,返回所用时间为
分钟,返回所用时间为![]() 分钟,
分钟,
所以总用氧量![]() ,
,![]() ;
;
(2)因为![]() ,由(1)得
,由(1)得![]() , 当且仅当
, 当且仅当![]() ,即
,即![]() 时,等号成立,即
时,等号成立,即![]() ;
;
令![]()
当![]() 时,任取
时,任取![]() ,且
,且![]() ,
,
则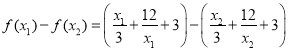
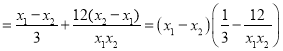 ,
,
因为![]() ,所以
,所以![]() ,
,![]() ,
,
因此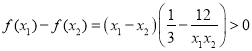 ,
,
所以函数![]() 在
在![]() 上单调递减;
上单调递减;
同理,![]() 在
在![]() 上单调递增;
上单调递增;
又![]() ,
,![]() ,
,![]() ,
,
所以![]() ,
,
即![]() ,所以总用氧量
,所以总用氧量![]() 的取值范围为
的取值范围为![]() .
.

【题目】某学校高三年级有学生1000名,经调查,其中750名同学经常参加体育锻炼(称为A类同学),另外250名同学不经常参加体育锻炼(称为B类同学),现用分层抽样方法(按A类、B类分两层)从该年级的学生中抽查100名同学.如果以身高达到165厘米作为达标的标准,对抽取的100名学生进行统计,得到以下列联表:
身高达标 | 身高不达标 | 总计 | |
积极参加体育锻炼 | 40 | ||
不积极参加体育锻炼 | 15 | ||
总计 | 100 |
(1)完成上表;
(2)能否有犯错率不超过0.05的前提下认为体育锻炼与身高达标有关系?(![]() 的观测值精确到0.001).
的观测值精确到0.001).
参考公式:![]() ,
,
参考数据:
P(K2≥k) | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.001 |
k | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
