题目内容
【题目】已知a>2,求证:loga(a-1)<log(a+1)a.
【答案】【解答】
证明:∵a>2,∴a-1>1.∴loga(a-1)>0,log(a+1)a>0,
由于![]()
![]()
![]() .
.
∵a>2,∴0<loga(a2-1)<logaa2=2.
∴ ![]() ,
,
即![]() .
.
∵log(a+1)a>0,∴loga(a-1)<log(a+1)a.
【解析】本题考查作商比较法的应用,解答本题需要先判断不等式两侧代数式的符号,然后再用作商法比较左右两侧的大小.(1)当不等式的两边为对数式或指数式时,可用作商比较法来证明,另外,要比较的两个解析式均为正值,且不宜采用作差比较法时,也常用作商比较法.(2)在作商比较法中 ![]() 是不正确的,这与a、b的符号有关,比如若b>0,由
是不正确的,这与a、b的符号有关,比如若b>0,由 ![]() ,可得a>b,但若b<0,则由
,可得a>b,但若b<0,则由 ![]() 得出的反而是a<b,也就是说,在作商比较法中,要对a、b的符号作出判断,否则,结论将是错误的.对于此类问题,不外乎可分为含参数变量的和大小固定的两类,因而也可以通过特殊值的方法进行一定的猜测,进而给出一定的理性推理或证明过程.
得出的反而是a<b,也就是说,在作商比较法中,要对a、b的符号作出判断,否则,结论将是错误的.对于此类问题,不外乎可分为含参数变量的和大小固定的两类,因而也可以通过特殊值的方法进行一定的猜测,进而给出一定的理性推理或证明过程.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
【题目】某电脑公司有6名产品推销员,其工作年限与年推销金额数据如下表:
推销员编号 | 1 | 2 | 3 | 4 | 5 |
工作年限x年 | 3 | 5 | 6 | 7 | 9 |
年推销金额y万元 | 2 | 3 | 3 | 4 | 5 |
(1)从编号1﹣5的五位推销员中随机取出两位,求他们年推销金额之和不少于7万元的概率;
(2)求年推销金额y关于工作年限x的线性回归方程 ![]() =
= ![]() x+
x+ ![]() ;若第6名产品推销员的工作年限为11年,试估计他的年推销金额. 附:回归直线的斜率和截距的最小二乘法估计公式为:
;若第6名产品推销员的工作年限为11年,试估计他的年推销金额. 附:回归直线的斜率和截距的最小二乘法估计公式为: ![]() =
= 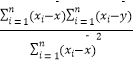 ,
, ![]() =
= ![]() ﹣
﹣ ![]()
![]() .
.