题目内容
【题目】已知数列{bn}满足bn=| ![]() |,其中a1=2,an+1=
|,其中a1=2,an+1= ![]()
(1)求b1 , b2 , b3 , 并猜想bn的表达式(不必写出证明过程);
(2)设cn= ![]() ,数列|cn|的前项和为Sn , 求证Sn<
,数列|cn|的前项和为Sn , 求证Sn< ![]() .
.
【答案】
(1)解:由a1=2,an+1= ![]() 可得:a2=
可得:a2= ![]() ,a3=
,a3= ![]() .又bn=|
.又bn=| ![]() |,
|,
则b1=4,b2=8,b3=16.
猜想bn=4×2n﹣1=2n+1
(2)解:证明:cn= ![]() =
= ![]() =
= ![]() ﹣
﹣ ![]() ,
,
∴数列|cn|的前项和为Sn= ![]() +
+ ![]() +…+
+…+ ![]() =
= ![]() .
.
∴Sn< ![]()
【解析】(1)由a1=2,an+1= ![]() 可得:a2=
可得:a2= ![]() ,a3=
,a3= ![]() .又bn=|
.又bn=| ![]() |,可得b1 , b2 , b3 . 猜想bn=2n+1 . (2)cn=
|,可得b1 , b2 , b3 . 猜想bn=2n+1 . (2)cn= ![]() =
= ![]() =
= ![]() ﹣
﹣ ![]() ,即可得出数列|cn|的前项和为Sn .
,即可得出数列|cn|的前项和为Sn .
【考点精析】掌握数列的定义和表示和数列的前n项和是解答本题的根本,需要知道数列中的每个数都叫这个数列的项.记作an,在数列第一个位置的项叫第1项(或首项),在第二个位置的叫第2项,……,序号为n的项叫第n项(也叫通项)记作an;数列{an}的前n项和sn与通项an的关系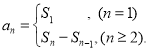 .
.

 阅读快车系列答案
阅读快车系列答案【题目】某单位N名员工参加“社区低碳你我他”活动.他们的年龄在25岁至50岁之间.按年龄分组:第1组[25,30),第2组[30,35),第3组[35,40),第4组[40,45),第5组[45,50],得到的频率分布直方图如图所示.下表是年龄的频率分布表.
区间 | [25,30) | [30,35) | [35,40) | [40,45) | [45,50] |
人数 | 25 | a | b |
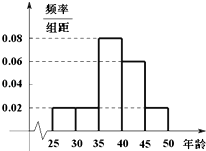
(1)求正整数a,b,N的值;
(2)现要从年龄较小的第1,2,3组中用分层抽样的方法抽取6人,则年龄在第1,2,3组的人数分别是多少?
(3)在(2)的条件下,从这6人中随机抽取2人参加社区宣传交流活动,求恰有1人在第3组的概率.