题目内容
【题目】已知椭圆E: ![]() +
+ ![]() =1的焦点在x轴上,A是E的左顶点,斜率为k(k>0)的直线交E于A,M两点,点N在E上,MA⊥NA.
=1的焦点在x轴上,A是E的左顶点,斜率为k(k>0)的直线交E于A,M两点,点N在E上,MA⊥NA.
(Ⅰ)当t=4,|AM|=|AN|时,求△AMN的面积;
(Ⅱ)当2|AM|=|AN|时,求k的取值范围.
【答案】解:(Ⅰ)方法一、t=4时,椭圆E的方程为 ![]() +
+ ![]() =1,A(﹣2,0),
=1,A(﹣2,0),
直线AM的方程为y=k(x+2),代入椭圆方程,整理可得(3+4k2)x2+16k2x+16k2﹣12=0,
解得x=﹣2或x=﹣ ![]() ,则|AM|=
,则|AM|= ![]() |2﹣
|2﹣ ![]() |=
|= ![]()
![]() ,
,
由AN⊥AM,可得|AN|= ![]()
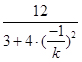 =
= ![]()
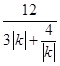 ,
,
由|AM|=|AN|,k>0,可得 ![]()
![]() =
= ![]()
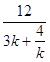 ,
,
整理可得(k﹣1)(4k2+k+4)=0,由4k2+k+4=0无实根,可得k=1,
即有△AMN的面积为 ![]() |AM|2=
|AM|2= ![]() (
( ![]()
![]() )2=
)2= ![]() ;
;
方法二、由|AM|=|AN|,可得M,N关于x轴对称,
由MA⊥NA.可得直线AM的斜率为1,直线AM的方程为y=x+2,
代入椭圆方程 ![]() +
+ ![]() =1,可得7x2+16x+4=0,
=1,可得7x2+16x+4=0,
解得x=﹣2或﹣ ![]() ,M(﹣
,M(﹣ ![]() ,
, ![]() ),N(﹣
),N(﹣ ![]() ,﹣
,﹣ ![]() ),
),
则△AMN的面积为 ![]() ×
× ![]() ×(﹣
×(﹣ ![]() +2)=
+2)= ![]() ;
;
(Ⅱ)直线AM的方程为y=k(x+ ![]() ),代入椭圆方程,
),代入椭圆方程,
可得(3+tk2)x2+2t ![]() k2x+t2k2﹣3t=0,
k2x+t2k2﹣3t=0,
解得x=﹣ ![]() 或x=﹣
或x=﹣ ![]() ,
,
即有|AM|= ![]() |
| ![]() ﹣
﹣ ![]() |=
|= ![]()
![]() ,
,
|AN|═ ![]()
![]() =
= ![]()
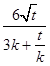 ,
,
由2|AM|=|AN|,可得2 ![]()
![]() =
= ![]()
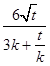 ,
,
整理得t= ![]() ,
,
由椭圆的焦点在x轴上,则t>3,即有 ![]() >3,即有
>3,即有 ![]() <0,
<0,
可得 ![]() <k<2,即k的取值范围是(
<k<2,即k的取值范围是( ![]() ,2)
,2)
【解析】(Ⅰ)方法一、求出t=4时,椭圆方程和顶点A,设出直线AM的方程,代入椭圆方程,求交点M,运用弦长公式求得|AM|,由垂直的条件可得|AN|,再由|AM|=|AN|,解得k=1,运用三角形的面积公式可得△AMN的面积;方法二、运用椭圆的对称性,可得直线AM的斜率为1,求得AM的方程代入椭圆方程,解方程可得M,N的坐标,运用三角形的面积公式计算即可得到;(Ⅱ)直线AM的方程为y=k(x+ ![]() ),代入椭圆方程,求得交点M,可得|AM|,|AN|,再由2|AM|=|AN|,求得t,再由椭圆的性质可得t>3,解不等式即可得到所求范围.
),代入椭圆方程,求得交点M,可得|AM|,|AN|,再由2|AM|=|AN|,求得t,再由椭圆的性质可得t>3,解不等式即可得到所求范围.

【题目】某校举行高二理科学生的数学与物理竞赛,并从中抽取72名学生进行成绩分析,所得学生的及格情况统计如表:
物理及格 | 物理不及格 | 合计 | |
数学及格 | 28 | 8 | 36 |
数学不及格 | 16 | 20 | 36 |
合计 | 44 | 28 | 72 |
(1)根据表中数据,判断是否是99%的把握认为“数学及格与物理及格有关”;
(2)若以抽取样本的频率为概率,现在该校高二理科学生中,从数学及格的学生中随机抽取3人,记X为这3人中物理不及格的人数,从数学不及格学生中随机抽取2人,记Y为这2人中物理不及格的人数,记ξ=|X﹣Y|,求ξ的分布列及数学期望. 附:x2= ![]() .
.
P(X2≥k) | 0.150 | 0.100 | 0.050 | 0.010 |
k | 2.072 | 2.706 | 3.841 | 6.635 |