Question

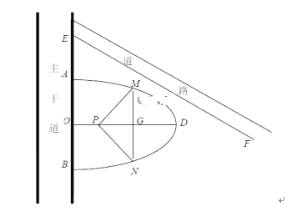
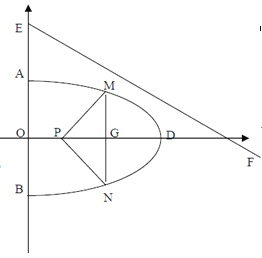
【题目】某学校决定在主干道旁边挖一个半椭圆形状的小湖，如图所示，AB=4，O为AB的中点，椭圆的焦点P在对称轴OD上，M、N在椭圆上，MN平行AB交OD与G，且G在P的右侧，△MNP为灯光区，用于美化环境.

(1)若学校的另一条道路EF满足OE=3，tan∠OEF=2，为确保道路安全，要求椭圆上任意一点到道路EF的距离都不小于，求半椭圆形的小湖的最大面积：(椭圆()的面积为)

(2)若椭圆的离心率为，要求灯光区的周长不小于，求PG的取值范围.

Answer 1

【答案】（1）；（2）.

【解析】

（1）由的长求得的值.首先求出直线所在的直线方程，设出与此直线平行，且与半椭圆相切的直线方程，利用两平行线间的距离求得相切直线的方程，代入椭圆方程利用判别式等于零求得的值.（2）根据椭圆的离心率和的值，利用求得的值，即求得椭圆方程，求得焦点的坐标.设出点的坐标，代入椭圆方程，由此写出周长的表达式，列不等式，解不等式可求得点横坐标的取值范围，减去后得到的取值范围.

（1）因为，所以直线的斜率为，

所以所在的直线方程为。

因为椭圆上任意一点到道路的距离都小于，

所以椭圆最大面积时与一条平行于且距离为的直线相切，

设直线，

由两条直线之间的距离为，所以，

解得或（舍弃）

设椭圆方程为，

由于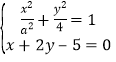得到

因为直线与椭圆相切，所以，解得，

所以椭圆方程为，

所以椭圆分面积为。

（2）设椭圆方程为，

因为椭圆的离心率为，所以，所以。

所以椭圆方程为

设，则灯光区的周长

由题意，

所以，所以

∴ ，

所以，即，

又因为在的右侧，所以，所以

所以的取值范围是。