Question

【题目】将正方形ABCD沿对角线BD折成直二面角A-BD-C，下列结论正确的是（ ）

A.AC⊥BDB.△ACD是等边三角形

C.AB与平面BCD成角D.AB与CD所成的角是60°

Answer 1

【答案】ABD

【解析】

首先画出几何体，由线面垂直的性质定理判断A是否正确；根据直二面角的条件计算的长度，判断是否是等边三角形；根据线面角的定义判断C；由异面直线所成的角转化为相交直线所成的角，取的中点，连结，转化为求或其补角.

A.取的中点，连结,由条件可知，又，

所有平面，平面，所有,所以A正确；

B.设正方形边长为2，则，且，所有，所以是等边三角形，所以B正确；

C.由条件可知平面，所以与平面所成的角为，所以C不正确；

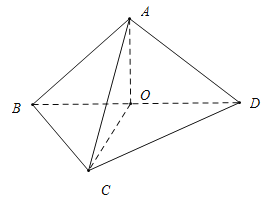
D.取的中点，连结，则，则所成的角是或其补角，由以上说明可知，,

所以是等边三角形，所以，故AB与CD所成的角是60°，所以D正确.

综上可知：ABD正确.

故选：ABD