Question

【题目】已知椭圆C的方程为，为椭圆C的左右焦点，离心率为，短轴长为2。

（1）求椭圆C的方程；

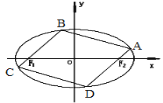
（2）如图，椭圆C的内接平行四边形ABCD的一组对边分别过椭圆的焦点，求该平行四边形ABCD面积的最大值．

Answer 1

【答案】(1) (2) 2

【解析】

（1）由题意可得2b=2，结合椭圆的离心率，求得的值，得到椭圆的方程；

（2）求出直线AD与轴垂直时平行四边形ABCD面积的值为，再设出AD所在直线斜率存在时的直线方程，联立直线方程和椭圆方程，求出AD的长度，再求出两平行线间的距离，代入平行四边形面积公式，可得平行四边形ABCD面积小于，从而求得结果.

（1）依题意得2b=2，，解得，

所以椭圆C的方程为。

（2）当AD所在直线与轴垂直时，则AD所在直线方程为x=1，

联立，解得y=，

此时平行四边形ABCD的面积S=2；

当AD所在的直线斜率存在时，设直线方程为y=k(x-1)，

联立，得，

设A()D()，则，

则，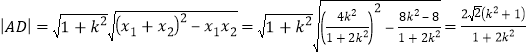

两条平行线间的距离，则平行四边形ABCD的面积，

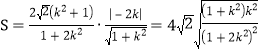令t=，

则S=，，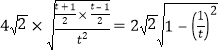

开口向下，关于单调递减，则，

综上所述，平行四边形ABCD的面积的最大值为。