题目内容
【题目】已知椭圆![]() :
:![]() 的短轴长为2,以椭圆
的短轴长为2,以椭圆![]() 的长轴为直径的圆与直线
的长轴为直径的圆与直线![]() 相切.
相切.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)斜率为![]() 的直线
的直线![]() 交椭圆
交椭圆![]() 于
于![]() ,
,![]() 两点,且
两点,且![]() ,若直线
,若直线![]() 上存在点
上存在点![]() ,使得
,使得![]() 是以
是以![]() 为顶角的等腰直角三角形,求直线
为顶角的等腰直角三角形,求直线![]() 的方程.
的方程.
【答案】(1)![]() ;(2)
;(2)![]()
【解析】
(1)先由短轴长求出![]() 的值,再根据点到直线的距离公式求出
的值,再根据点到直线的距离公式求出![]() 的值即可;(2)设直线
的值即可;(2)设直线![]() 的方程为
的方程为![]() ,先由
,先由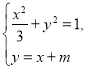 得
得![]() ,则
,则![]() ,
,![]() ,再根据直线
,再根据直线![]() 上存在点
上存在点![]() ,使得
,使得![]() 是以
是以![]() 为顶角的等腰直角三角形,得出
为顶角的等腰直角三角形,得出![]() ,最后由方程组
,最后由方程组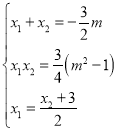 即可求出
即可求出![]() 的值进而求出直线
的值进而求出直线![]() 的方程.
的方程.
(1)由题意得![]() ,
,![]() ,则
,则![]() ,所以椭圆
,所以椭圆![]() 的方程为
的方程为![]() .
.
(2)设直线![]() 的方程为
的方程为![]() ,
,![]() ,
,
由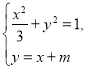 得
得![]() .
.
令![]() ,得
,得![]() ,则
,则![]() ,
,![]() .
.
因为![]() 是以
是以![]() 为顶角的等腰直角三角形,
为顶角的等腰直角三角形,
所以![]() 平行于
平行于![]() 轴,过
轴,过![]() 作
作![]() 的垂线,则垂足
的垂线,则垂足![]() 为线段
为线段![]() 的中点.
的中点.
设点![]() 的坐标为
的坐标为![]() ,则
,则![]() .
.
由方程组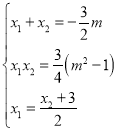 解得
解得![]() ,即
,即![]() .
.
而![]() ,所以直线
,所以直线![]() 的方程为
的方程为![]() .
.

【题目】第7届世界军人运动会于2019年10月18日至27日在湖北武汉举行,赛期10天,共设置射击、游泳、田径、篮球等27个大项,329个小项.共有来自100多个国家的近万名现役军人同台竞技.前期为迎接军运会顺利召开,武汉市很多单位和部门都开展了丰富多彩的宣传和教育活动,努力让大家更多的了解军运会的相关知识,并倡议大家做文明公民.武汉市体育局为了解广大民众对军运会知识的知晓情况,在全市开展了网上问卷调查,民众参与度极高,现从大批参与者中随机抽取200名幸运参与者,他们得分(满分100分)数据,统计结果如下:
组别 |
|
|
|
|
|
|
|
频数 | 5 | 30 | 40 | 50 | 45 | 20 | 10 |
(1)若此次问卷调查得分整体服从正态分布,用样本来估计总体,设![]() ,
,![]() 分别为这200人得分的平均值和标准差(同一组数据用该区间中点值作为代表),求
分别为这200人得分的平均值和标准差(同一组数据用该区间中点值作为代表),求![]() ,
,![]() 的值(
的值(![]() ,
,![]() 的值四舍五入取整数),并计算
的值四舍五入取整数),并计算![]() ;
;
(2)在(1)的条件下,为感谢大家参与这次活动,市体育局还对参加问卷调查的幸运市民制定如下奖励方案:得分低于![]() 的可以获得1次抽奖机会,得分不低于
的可以获得1次抽奖机会,得分不低于![]() 的可获得2次抽奖机会,在一次抽奖中,抽中价值为15元的纪念品A的概率为
的可获得2次抽奖机会,在一次抽奖中,抽中价值为15元的纪念品A的概率为![]() ,抽中价值为30元的纪念品B的概率为
,抽中价值为30元的纪念品B的概率为![]() .现有市民张先生参加了此次问卷调查并成为幸运参与者,记Y为他参加活动获得纪念品的总价值,求Y的分布列和数学期望,并估算此次纪念品所需要的总金额.
.现有市民张先生参加了此次问卷调查并成为幸运参与者,记Y为他参加活动获得纪念品的总价值,求Y的分布列和数学期望,并估算此次纪念品所需要的总金额.
(参考数据:![]() ;
;![]() ;
;![]() .)
.)