题目内容
【题目】已知函数f（x）＝|x﹣1|，关于x的不等式f（x）＜3﹣|2x+1|的解集记为A．
（1）求A；
（2）已知a，b∈A，求证：f（ab）＞f（a）﹣f（b）．
【答案】（1）{x∈R|﹣1＜x＜1}； （2）见解析.
【解析】
（1）分类讨论，去掉绝对值符号，即可求A；
（2）利用作差法，即可证明：f（ab）＞f（a）﹣f（b）．
（1）由f（x）＜3﹣|2x+1|，得|x﹣1|+|2x+1|＜3，
即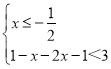
或
或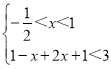
解得
或
，
所以，集合A＝{x∈R|﹣1＜x＜1}．
（2）∵a，b∈A，∴﹣1＜ab＜1，
∴f（ab）＝|ab﹣1|＝1﹣ab，f（a）＝|a﹣1|＝1﹣a，f（b）＝|b﹣1|＝1﹣b，
∵f（ab）﹣（f（a）﹣f（b））＝1﹣ab﹣1+a+1﹣b＝（1+a）（1﹣b）＞0，
∴f（ab）＞f（a）﹣f（b）．
练习册系列答案
阅读快车系列答案
相关题目
