题目内容
7.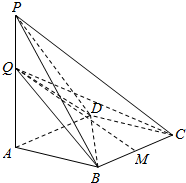 已知四棱锥P-ABCD中,底面ABCD为∠ABC=$\frac{2}{3}$π的菱形,PA⊥平面ABCD,点Q在直线PA上.
已知四棱锥P-ABCD中,底面ABCD为∠ABC=$\frac{2}{3}$π的菱形,PA⊥平面ABCD,点Q在直线PA上.(1)证明直线QC⊥直线BD;
(2)若二面角B-QC-D的大小为$\frac{2π}{3}$,点M为BC的中点,求直线QM与AB所成角的余弦值.
分析 (1)连结AC,由菱形性质得BD⊥AC,由线面垂直得PA⊥BD,由此能证明直线QC⊥直线BD.
(2)由对称性得二面角B-QC-A的大小为$\frac{π}{3}$,设底面ABCD的棱长为2,AQ=x,设AC、BD交于点E,过点E做QC的垂线,垂足设为F,过点M作AB的平行线交AD的中点为G,由此利用余弦定理能求出QM与AB所成角的余弦值.
解答  (1)证明:连结AC,∵底面ABCD为∠ABC=$\frac{2}{3}$π的菱形,∴BD⊥AC,
(1)证明:连结AC,∵底面ABCD为∠ABC=$\frac{2}{3}$π的菱形,∴BD⊥AC,
∵PA⊥平面ABCD,BD?平面ABCD,∴PA⊥BD,
∵PA∩AC=A,∴BD⊥平面PAC,
∵QC?平面PAC,∴直线QC⊥直线BD.
(2)解:∵二面角B-QC-D的大小为$\frac{2π}{3}$,∴由对称性得二面角B-QC-A的大小为$\frac{π}{3}$,
设底面ABCD的棱长为2,AQ=x,设AC、BD交于点E,
则点B到平面AQC的距离BE为1,过点E做QC的垂线,垂足设为F,
则有tan∠BFE=tan$\frac{π}{3}$=$\frac{BE}{EF}$,BE=1,则EF=$\frac{\sqrt{3}}{3}$,点A到QC的距离为$\frac{2\sqrt{3}}{3}$,
则有$\frac{2\sqrt{3}}{3}•\sqrt{{x}^{2}+(2\sqrt{3})^{2}}$=$x•2\sqrt{3}$,解得x=$\frac{\sqrt{6}}{2}$.
过点M作AB的平行线交AD的中点为G,
则GM=2,QG=$\sqrt{(\frac{\sqrt{6}}{2})^{2}+{1}^{2}}$=$\frac{\sqrt{10}}{2}$,AM=$\sqrt{{2}^{2}+{1}^{2}+2×1×1×\frac{1}{2}}$=$\sqrt{7}$,
∴QM=$\sqrt{(\frac{\sqrt{6}}{2})^{2}+(\sqrt{7})^{2}}$=$\frac{\sqrt{34}}{2}$,
∴cos∠QMG=$\frac{Q{M}^{2}+G{M}^{2}-Q{G}^{2}}{2×QM×GM}$=$\frac{\frac{34}{4}+4-\frac{10}{4}}{2×\frac{\sqrt{34}}{2}×2}$=$\frac{5\sqrt{34}}{34}$,
∴所求的QM与AB所成角的余弦值为$\frac{5\sqrt{34}}{34}$.
点评 本题考查异面直线垂直的证明,考查两直线所成角的余弦值的求法,是中档题,解题时要认真审题,注意余弦定理的合理运用.

 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案| A. | f(x)=x2-2x-3 | B. | f(x)=x2+2x-3 | C. | f(x)=x2-2x+3 | D. | f(x)=x2+2x+3 |
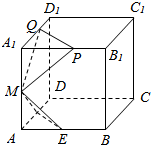 如图:已知棱长为l的正方体ABCD-A1B1C1D1中,E,F,M分别是AB、AD、AA1的中点,又P、Q分别在线段A1B1、A1D1上,且A1P=A1Q=x,0<x<1,设平面MEF∩平面MPQ=l,则下列结论中不成立的是( )
如图:已知棱长为l的正方体ABCD-A1B1C1D1中,E,F,M分别是AB、AD、AA1的中点,又P、Q分别在线段A1B1、A1D1上,且A1P=A1Q=x,0<x<1,设平面MEF∩平面MPQ=l,则下列结论中不成立的是( )| A. | l∥平面ABCD | B. | 平面MEF与平面MPQ不垂直 | ||
| C. | l⊥BC1 | D. | 当x变化时,l是定直线 |
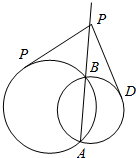 如图,两圆相交于A、B两点,P为两圆公共弦AB上任一点,从P引两圆的切线PC、PD,若PC=2$\sqrt{2}$cm,则PD=2$\sqrt{2}$cm.
如图,两圆相交于A、B两点,P为两圆公共弦AB上任一点,从P引两圆的切线PC、PD,若PC=2$\sqrt{2}$cm,则PD=2$\sqrt{2}$cm. 如图,准备在扇形空地AOB上修建一个山水景观OPQ,己知∠AOB=$\frac{2}{3}$π,OA=lkm,点P在扇形弧上,PQ∥OA交OB于点Q,记∠POA=x.
如图,准备在扇形空地AOB上修建一个山水景观OPQ,己知∠AOB=$\frac{2}{3}$π,OA=lkm,点P在扇形弧上,PQ∥OA交OB于点Q,记∠POA=x.