题目内容
14.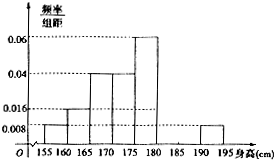 从某校的800名男生中随机抽取50人测量身高,被测学生身高介于介于155cm和195cm之间,将测量结果按如下方式分成八组:第一组[155,160),第二组[160,165),…..,第八组[190,195],如图是按上述分组方法得到的频率分布直方图的一部分,已知第一组与第八组人数相同,第六组的人数为4人.
从某校的800名男生中随机抽取50人测量身高,被测学生身高介于介于155cm和195cm之间,将测量结果按如下方式分成八组:第一组[155,160),第二组[160,165),…..,第八组[190,195],如图是按上述分组方法得到的频率分布直方图的一部分,已知第一组与第八组人数相同,第六组的人数为4人.(Ⅰ)求第七组的频率并估计该校男生中身高在180cm以上(含180cm)的人数;
(Ⅱ)从第六组和第八组的男生中随机抽取2名,求他们的身高之差大于5cm的概率.
分析 (I)根据直方图得出第6组的频率,
运用对立事件的概率求解得出:第7组的频率,
再根据与总体的关系得出0.18×800计算即可
(II)第六组[180,185)的人数为4人,设为a,b,c,d;
第八组[190,195]的人数为2人,设为A,B;
列举事件,根据题意判断个数,运用古典概率计算公式即可.
解答 解:(I)第六组的频率为$\frac{4}{50}$=0.08,
所以第七组的频率为1-0.08-5×(0.008×2+0.016+0.04×2+0.06)=0.06;
由直方图得后三组频率为0.06+0.08+0.008×5=0.18,
所以800名男生中身高在180cm以上的人数为0.18×800=144人,
(II)第六组[180,185)的人数为4人,设为a,b,c,d;
第八组[190,195]的人数为2人,设为A,B;
则从第六组,第八组的男生中随机抽取2名男生有:ab,ac,ad,bc,bd,cd,aA,bA,cA.dA,aB,bB,cB,dB,AB,共15种情况.
设从“他们的身高之差大于5cm”为事件M,所以该事件包含的基本事件为aA,bA,cA.dA,aB,bB,cB,dB共8种情况.
故P(A)=$\frac{8}{15}$
点评 本题考查了频率直方图的运用,列举法求解基本事件,根据古典概率公式求解,具体设出事件,表示出来是本题的关键.

练习册系列答案
 优生乐园系列答案
优生乐园系列答案 新编小学单元自测题系列答案
新编小学单元自测题系列答案
相关题目
5.设函数f(x)=x3+3ax2+3bx有两个极值点x1、x2,且x1∈[-1,0],x2∈[1,2],则点(a,b)在aOb平面上所构成区域的面积为( )
| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | $\frac{3}{4}$ | D. | 1 |
 如图,在直三棱柱ABC-A1B1C1中,底面为正三角形,点M在棱BB1上,AB=4,AA1=5,
如图,在直三棱柱ABC-A1B1C1中,底面为正三角形,点M在棱BB1上,AB=4,AA1=5,