题目内容
4.对于任意正整数n,定义“n!!”如下:当n是偶数时,n!!=n•(n-2)•(n-4)…6•4•2,当n是奇数时,n!!=n•(n-2)•(n-4)…5•3•1,且有n!=n•(n-1)•(n-2)…3•2•1则有四个命题:①(2015!!)•(2016!!)=2016!
②2016!!=22018×1008!
③2015!!的个位数是5
④2014!!的个位数是0
其中正确的命题有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
分析 利用双阶乘的定义判断各个命题是解决该题的关键.关键要理解好双阶乘的定义,把握好双阶乘是哪些数的连乘积.
解答 解:根据题意,依次分析四个命题可得:
对于①,(2015!!)•(2016!!)=(2•4•6•8…2008•2010•2012•2014•2016)•(1•3•5•7…2009•2011•2013•2015)=1•2•3•4•5…•2012•2013•2014•2015•2016=2016!,故①正确;
对于②,2016!!=2•4•6•8•10…2008•2010•2012•2014•2016=21008(1•2•3•4…1008)=21008•1008!,故②正确;
对于③,2015!=2015×2011×2009×…×3×1,其个位数字与1×3×5×7×9的个位数字相同,故其个位数字为5,故正确;
对于④,2014!!=2•4•6•8…2008•2010•2012•2014,其中含有10,故个位数字为0,故正确;
故选:D.
点评 本题考查新定义型问题的求解思路与方法,考查新定义型问题的理解与转化方法,体现了数学中的转化与化归的思想方法.注意与学过知识间的联系.

练习册系列答案
相关题目
16.我们把有相同数字相邻的数叫“兄弟数”,现从由一个1、一个2、两个3、两个4这六个数字组成的所有不同的六位数中随机抽取一个,则抽到“兄弟数”的概率为( )
| A. | $\frac{2}{5}$ | B. | $\frac{7}{15}$ | C. | $\frac{8}{15}$ | D. | $\frac{3}{5}$ |
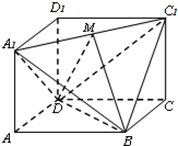
 如图,在三棱锥P-ABC中,PA⊥底面ABC,AB⊥BC,AB=PA=BC=2.D,E分别为AB,AC的中点,过DE的平面与PB,PC相交于点M,N(M与P,B不重合,N与P,C不重合).
如图,在三棱锥P-ABC中,PA⊥底面ABC,AB⊥BC,AB=PA=BC=2.D,E分别为AB,AC的中点,过DE的平面与PB,PC相交于点M,N(M与P,B不重合,N与P,C不重合).
 如图,四棱锥S-ABCD中,AB∥CD,BC⊥CD,侧面SAB为等边三角形,AB=BC=2,CD=1,SD=$\sqrt{7}$.
如图,四棱锥S-ABCD中,AB∥CD,BC⊥CD,侧面SAB为等边三角形,AB=BC=2,CD=1,SD=$\sqrt{7}$. 如图,在直三棱柱ABC-A1B1C1中,AB=BC=2,∠ABC=120°,D为AC的中点,P为棱A1B上的动点.
如图,在直三棱柱ABC-A1B1C1中,AB=BC=2,∠ABC=120°,D为AC的中点,P为棱A1B上的动点.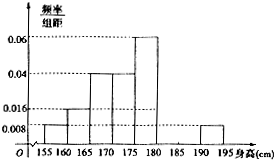 从某校的800名男生中随机抽取50人测量身高,被测学生身高介于介于155cm和195cm之间,将测量结果按如下方式分成八组:第一组[155,160),第二组[160,165),…..,第八组[190,195],如图是按上述分组方法得到的频率分布直方图的一部分,已知第一组与第八组人数相同,第六组的人数为4人.
从某校的800名男生中随机抽取50人测量身高,被测学生身高介于介于155cm和195cm之间,将测量结果按如下方式分成八组:第一组[155,160),第二组[160,165),…..,第八组[190,195],如图是按上述分组方法得到的频率分布直方图的一部分,已知第一组与第八组人数相同,第六组的人数为4人.