题目内容
19.记集合A={(x,y)|(x-1)2+y2≤1},B={(x,y)|$\left\{\begin{array}{l}{x≥0}\\{y≤x}\\{y≥{x}^{2}}\end{array}\right.$},构成的平面区域分别为M,N,现随机地向M中抛一粒豆子(大小忽略不计),则该豆子落入N中的概率为$\frac{1}{6π}$.分析 求出集合A={(x,y)|(x-1)2+y2≤1},B={(x,y)|$\left\{\begin{array}{l}{x≥0}\\{y≤x}\\{y≥{x}^{2}}\end{array}\right.$},表示的区域的面积,即可求得豆子落入N中的概率.
解答 解:集合A={(x,y)|(x-1)2+y2≤1},表示的区域的面积为π;
B={(x,y)|$\left\{\begin{array}{l}{x≥0}\\{y≤x}\\{y≥{x}^{2}}\end{array}\right.$},表示的区域的面积为${∫}_{0}^{1}(x-{x}^{2})dx$=$(\frac{1}{2}{x}^{2}-\frac{1}{3}{x}^{3})$${|}_{0}^{1}$=$\frac{1}{6}$,
∴该豆子落入N中的概率为$\frac{1}{6π}$.
故答案为:$\frac{1}{6π}$.
点评 本题考查概率的计算,正确求出面积是关键.

练习册系列答案
 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
 如图,四棱锥S-ABCD中,AB∥CD,BC⊥CD,侧面SAB为等边三角形,AB=BC=2,CD=1,SD=$\sqrt{7}$.
如图,四棱锥S-ABCD中,AB∥CD,BC⊥CD,侧面SAB为等边三角形,AB=BC=2,CD=1,SD=$\sqrt{7}$.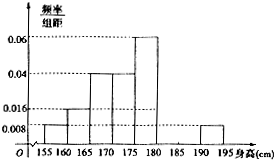 从某校的800名男生中随机抽取50人测量身高,被测学生身高介于介于155cm和195cm之间,将测量结果按如下方式分成八组:第一组[155,160),第二组[160,165),…..,第八组[190,195],如图是按上述分组方法得到的频率分布直方图的一部分,已知第一组与第八组人数相同,第六组的人数为4人.
从某校的800名男生中随机抽取50人测量身高,被测学生身高介于介于155cm和195cm之间,将测量结果按如下方式分成八组:第一组[155,160),第二组[160,165),…..,第八组[190,195],如图是按上述分组方法得到的频率分布直方图的一部分,已知第一组与第八组人数相同,第六组的人数为4人. 已知直三棱柱ABC-A′B′C′满足∠BAC=90°,AB=AC=$\frac{1}{2}$AA′=2,点M、N分别为A′B,B′C′的中点.
已知直三棱柱ABC-A′B′C′满足∠BAC=90°,AB=AC=$\frac{1}{2}$AA′=2,点M、N分别为A′B,B′C′的中点.