题目内容
6．若数列{an}为等差数列，Sn为其前n项和，S5=S6，公差d=-2．（1）求数列{an}的通项公式；
（2）已知{bn}是公比为正的等比数列，b1=a5，b3=$\frac{1}{3}（{a}_{1}+{a}_{2}+{a}_{3}）$，求数列{bn}的通项公式．
分析 （1）通过a6=S6-S5及数列{an}的公差d=-2，计算即可；
（2）通过（1）直接计算可得b1、b3的值，利用q2=$\frac{{b}_{3}}{{b}_{1}}$及q＞0，计算即得结论．
解答 解：（1）∵S5=S6，∴a6=S6-S5=0，
又∵数列{an}为等差数列，公差d=-2，
∴a1=a6-5d=0-5×（-2）=10，
∴数列{an}的通项an=10-2（n-1）=12-2n；
（2）∵an=12-2n，∴b1=a5=2，
∴b3=$\frac{1}{3}$S3=$\frac{1}{3}（{a}_{1}+{a}_{2}+{a}_{3}）$=8，
又∵数列{bn}是公比为q的等比数列，
∴q2=$\frac{{b}_{3}}{{b}_{1}}$=$\frac{8}{2}$=4，
又∵公比q＞0，∴q=2，
∴数列{bn}的通项bn=2×2n-1=2n．
点评 本题考查等差数列的简单性质及其通项公式，考查等比数列的简单性质及其通项公式，注意解题方法的积累，属于中档题．
练习册系列答案
相关题目
16．我们把有相同数字相邻的数叫“兄弟数”，现从由一个1、一个2、两个3、两个4这六个数字组成的所有不同的六位数中随机抽取一个，则抽到“兄弟数”的概率为（ ）
| A． | $\frac{2}{5}$ | B． | $\frac{7}{15}$ | C． | $\frac{8}{15}$ | D． | $\frac{3}{5}$ |
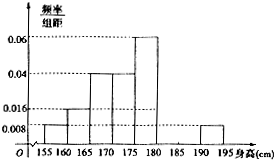从某校的800名男生中随机抽取50人测量身高，被测学生身高介于介于155cm和195cm之间，将测量结果按如下方式分成八组：第一组[155，160），第二组[160，165），…..，第八组[190，195]，如图是按上述分组方法得到的频率分布直方图的一部分，已知第一组与第八组人数相同，第六组的人数为4人．