题目内容
5.设函数f(x)=x3+3ax2+3bx有两个极值点x1、x2,且x1∈[-1,0],x2∈[1,2],则点(a,b)在aOb平面上所构成区域的面积为( )| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | $\frac{3}{4}$ | D. | 1 |
分析 根据极值的意义可知,极值点x1、x2是导函数等于零的两个根,根据根的分布建立不等关系,画出满足条件的区域,求解面积即可;
解答 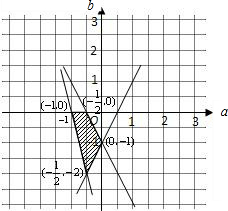 解:函数f(x)=x3+3ax2+3bx,可得f′(x)=3x2+6ax+3b,
解:函数f(x)=x3+3ax2+3bx,可得f′(x)=3x2+6ax+3b,
依题意知,方程f′(x)=0有两个根x1、x2,且x1∈[-1,0],x2∈[1,2]
等价于f′(-1)≥0,f′(0)≤0,f′(1)≤0,
f′(2)≥0.
由此得b,c满足的约束条件为$\left\{\begin{array}{l}b≥2a-1\\ b≤0\\ b≤-2a-1\\ b≥-4a-4\end{array}\right.$,
满足这些条件的点(a,b)的区域为图中阴影部分.
阴影部分的面积为:$\frac{1+\frac{1}{2}}{2}×2-\frac{1}{2}×\frac{1}{2}×1-\frac{1}{2}×\frac{1}{2}×1$=1.
故选:D.
点评 本题主要考查了利用导数研究函数的极值,以及二元一次不等式(组)与平面区域,是中档题.

练习册系列答案
 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案 培优三好生系列答案
培优三好生系列答案
相关题目
16.我们把有相同数字相邻的数叫“兄弟数”,现从由一个1、一个2、两个3、两个4这六个数字组成的所有不同的六位数中随机抽取一个,则抽到“兄弟数”的概率为( )
| A. | $\frac{2}{5}$ | B. | $\frac{7}{15}$ | C. | $\frac{8}{15}$ | D. | $\frac{3}{5}$ |
20.下列说法正确的是( )
| A. | 样本10,6,8,5,6的标准差是5.3 | |
| B. | “p∨q为真”是“p∧q为真”的充分不必要条件 | |
| C. | K2是用来判断两个分类变量是否相关的随机变量,当K2的值很小时可以推定两类变量不相关 | |
| D. | 设有一个回归直线方程为$\widehat{y}$=2-1.5x,则变量x毎增加一个单位,y平均减少1.5个单位 |
 如图,在三棱锥P-ABC中,PA⊥底面ABC,AB⊥BC,AB=PA=BC=2.D,E分别为AB,AC的中点,过DE的平面与PB,PC相交于点M,N(M与P,B不重合,N与P,C不重合).
如图,在三棱锥P-ABC中,PA⊥底面ABC,AB⊥BC,AB=PA=BC=2.D,E分别为AB,AC的中点,过DE的平面与PB,PC相交于点M,N(M与P,B不重合,N与P,C不重合). 如图,在直三棱柱ABC-A1B1C1中,AB=BC=2,∠ABC=120°,D为AC的中点,P为棱A1B上的动点.
如图,在直三棱柱ABC-A1B1C1中,AB=BC=2,∠ABC=120°,D为AC的中点,P为棱A1B上的动点.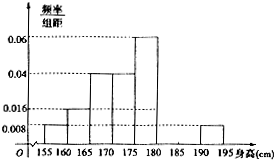 从某校的800名男生中随机抽取50人测量身高,被测学生身高介于介于155cm和195cm之间,将测量结果按如下方式分成八组:第一组[155,160),第二组[160,165),…..,第八组[190,195],如图是按上述分组方法得到的频率分布直方图的一部分,已知第一组与第八组人数相同,第六组的人数为4人.
从某校的800名男生中随机抽取50人测量身高,被测学生身高介于介于155cm和195cm之间,将测量结果按如下方式分成八组:第一组[155,160),第二组[160,165),…..,第八组[190,195],如图是按上述分组方法得到的频率分布直方图的一部分,已知第一组与第八组人数相同,第六组的人数为4人.