Question

【题目】已知函数的定义域为[－1，5]，部分对应值如下表，的导函数的图象如图所示，下列关于的命题正确的是（ ）

		0	4	5
	1	2	2	1

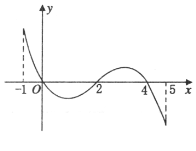
A.函数的极大值点为0，4；

B.函数在[0，2]上是减函数；

C.如果当时，的最大值是2，那么的最大值为4；

D.函数的零点个数可能为0、1、2、3、4个．

Answer 1

【答案】AB

【解析】

A由的导函数的图象知函数的极大值点为0，4；B由在，上导函数为负知B正确；由知，极小值（2）未知，无法判断函数有几个零点，D依照相应理论即可判断

解：对于A由的导函数的图象知，

函数的极大值点为0，4，故A正确；

对于B因为在，上导函数为负，

故函数在，上是减函数，故B正确；

对于C由表中数据可得当或时，函数取最大值2，

若，时，的最大值是2，那么，故的最大值为5，即C错误；

对于D函数在定义域为，共有两个单调增区间，两个单调减区间，即在和上单调递增，在和上单调递减，所以在或处取得极大值，在处取得极小值，令，即函数与的交点，

若，则

此时当或时两函数无交点，故函数无零点；

当时有一个交点，当或时有两个交点，当时有四个交点，

故函数的零点个数能为0、1、2、4个；

若，则，

此时当或时两函数无交点，当时有三个交点，当时有四个交点，当或时有两个交点，

故函数的零点个数能为0、2、3、4个，

若，则，

此时当或时两函数无交点，当时有三个交点，当时有四个交点，当时有两个交点，

故函数的零点个数能为0、2、3、4个，

故函数的零点个数不可能为0、1、2、3、4个，

故D错误．

故选：AB．