题目内容
【题目】如图，在正方体
中，点
在线段
上运动，则下列判断中正确的是（ ）
①平面
平面
；
②
平面
；
③异面直线
与
所成角的取值范围是
；
④三棱锥
的体积不变.
A. ①② B. ①②④ C. ③④ D. ①④
【答案】B
【解析】
①连接DB1，容易证明DB1⊥面ACD1 ，从而可以证明面面垂直；
②连接A1B，A1C1容易证明平面BA1C1∥面ACD1，从而由线面平行的定义可得；
③分析出A1P与AD1所成角的范围，从而可以判断真假；
④
=
，C到面 AD1P的距离不变，且三角形AD1P的面积不变；
对于①，连接DB1，根据正方体的性质，有DB1⊥面ACD1 ，DB1平面PB1D，从而可以证明平面PB1D⊥平面ACD1，正确．
②连接A1B，A1C1容易证明平面BA1C1∥面ACD1，从而由线面平行的定义可得 A1P∥平面ACD1，正确．
③当P与线段BC1的两端点重合时，A1P与AD1所成角取最小值
，
当P与线段BC1的中点重合时，A1P与AD1所成角取最大值
，
故A1P与AD1所成角的范围是
，错误；
④=，C到面AD1P的距离不变，且三角形AD1P的面积不变．
∴三棱锥A﹣D1PC的体积不变，正确；
正确的命题为①②④．
故选：B．
【题目】已知函数
的定义域为[－1，5]，部分对应值如下表，的导函数
的图象如图所示，下列关于的命题正确的是（ ）
|
| 0 | 4 | 5 |
| 1 | 2 | 2 | 1 |
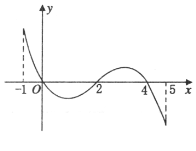
A.函数的极大值点为0，4；
B.函数在[0，2]上是减函数；
C.如果当
时，的最大值是2，那么
的最大值为4；
D.函数
的零点个数可能为0、1、2、3、4个．
【题目】为响应“文化强国建设”号召，并增加学生们对古典文学的学习兴趣，雅礼中学计划建设一个古典文学熏陶室.为了解学生阅读需求，随机抽取200名学生做统计调查.统计显示，男生喜欢阅读古典文学的有64人，不喜欢的有56人；女生喜欢阅读古典文学的有36人，不喜欢的有44人.
(1)能否在犯错误的概率不超过0.25的前提下认为喜欢阅读古典文学与性别有关系？
(2)为引导学生积极参与阅读古典文学书籍，语文教研组计划牵头举办雅礼教育集团古典文学阅读交流会.经过综合考虑与对比，语文教研组已经从这200人中筛选出了5名男生代表和4名女生代表，其中有3名男生代表和2名女生代表喜欢古典文学.现从这9名代表中任选3名男生代表和2名女生代表参加交流会，记
为参加交流会的5人中喜欢古典文学的人数，求的分布列及数学期望
.
附：
，其中
.
参考数据：
| 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 |
| 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 |
