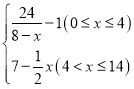题目内容
【题目】某市为了制定合理的节电方案,供电局对居民用电进行了调查,通过抽样,获得了某年200户居民每户的月均用电量(单位:度),将数据按照![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 分成9组,制成了如图所示的频率分布直方图.
分成9组,制成了如图所示的频率分布直方图.
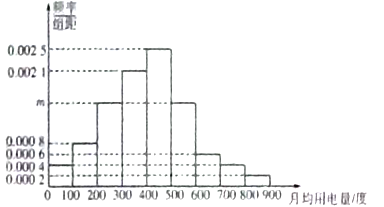
(Ⅰ)求直方图中![]() 的值并估计居民月均用电量的中位数;
的值并估计居民月均用电量的中位数;
(Ⅱ)现从第8组和第9组的居民中任选取2户居民进行访问,则两组中各有一户被选中的概率.
【答案】(Ⅰ)![]() .中位数为408度.(Ⅱ)
.中位数为408度.(Ⅱ) ![]() .
.
【解析】试题分析:(1)根据频率分布直方图,求解![]() 的值,即可求得前4组的频率之和,从而估计出居民的月均用电量的中位数;
的值,即可求得前4组的频率之和,从而估计出居民的月均用电量的中位数;
(2)计算出第8和第9组的户数,分别设为![]() 和
和![]() ,从而得到选出2户的基本事件的个数,进而得到两组中各有一户被选中的基本事件个数,利用古典概型的概率计算公式,即可求解概率。
,从而得到选出2户的基本事件的个数,进而得到两组中各有一户被选中的基本事件个数,利用古典概型的概率计算公式,即可求解概率。
试题解析:
解:(Ⅰ) ![]() ,
,
∴![]() .
.
设中位数是![]() 度,前5组的频率之和为
度,前5组的频率之和为![]() ,
,
而前4组的频率之和为![]() ,
,
所以![]() ,
, ![]() ,
,
故![]() ,即居民月均用电量的中位数为408度.
,即居民月均用电量的中位数为408度.
(Ⅱ)第8组的户数为![]() ,分别设为
,分别设为![]() ,
, ![]() ,
, ![]() ,
, ![]() ,第9组的户数为
,第9组的户数为![]() ,分别设为
,分别设为![]() ,
, ![]() ,则从中任选出2户的基本事件为
,则从中任选出2户的基本事件为![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 共15种.
共15种.
其中两组中各有一户被选中的基本事件为![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 共8种.
共8种.
所以第8,9组各有一户被选中的概率![]() .
.

练习册系列答案
相关题目