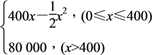Question

【题目】已知函数.

（1）当时，求不等式的解集；

（2）若，且，求证： .

Answer 1

【答案】(1) ;(2)4.

【解析】试题分析：（1）通过讨论的范围，得到关于的不等式组，解出求并集即可的结果；（2）

，然后根据基本不等式的性质证明即可.

试题解析：（Ⅰ）当时，不等式化为，

即或或，

解得或或，

∴不等式的解集为；

（Ⅱ）

当且仅当，即时“”成立，

所以.

【易错点晴】本题主要考查绝对值不等式的解法及利用基本不等式求最值，属于中档题.利用基本不等式求最值时，一定要正确理解和掌握“一正，二定，三相等”的内涵：一正是，首先要判断参数是否为正；二定是，其次要看和或积是否为定值（和定积最大，积定和最小）；三相等是，最后一定要验证等号能否成立（主要注意两点，一是相等时参数否在定义域内，二是多次用或时等号能否同时成立）.