Question

【题目】(1)已知直线方程为(2＋m)x＋(1－2m)y＋4－3m＝0，求证：不论m为何实数，此直线必过定点；

(2)过这定点引一直线，使它夹在两坐标轴间的线段被这点平分，求这条直线的方程.

Answer 1

【答案】（1）证明见解析；（2）2x＋y＋4＝0

【解析】试题分析：（1）直线方程整理得m(x－2y－3)＋2x＋y＋4＝0，所以，求出定点；（2）由(－1，－2)是线段AB的中点，得到A(-2,0)，B(0，-4)，写出直线方程。

试题解析：

(1)证明：直线方程可写为m(x－2y－3)＋2x＋y＋4＝0，

由，得，

∴点(－1，－2)适合方程(2＋m)x＋(1－2m)·y＋4－3m＝0，

因此，直线(2＋m)x＋(1－2m)y＋4－3m＝0过定点(－1，－2).

(2)设过点(－1，－2)所引的直线与x轴、y轴分别交于A(a,0)，B(0，b)点，

∵(－1，－2)是线段AB的中点，

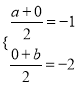∴，解得

∴所求直线方程为，即2x＋y＋4＝0.