题目内容
18.指数函数y=(a-1)x与$y={(\frac{1}{a})^x}$具有不同的单调性,比较m=${(a-1)^{\frac{1}{3}}}$与n=${(\frac{1}{a})^3}$的大小关系.分析 由指数函数y=(a-1)x与$y={(\frac{1}{a})^x}$具有不同的单调性,可得:$\left\{\begin{array}{l}a-1>1\\ 0<\frac{1}{a}<1\end{array}\right.$,或$\left\{\begin{array}{l}\frac{1}{a}>1\\ 0<a-1<1\end{array}\right.$,解得a的取值范围,结合幂函数的图象和性质,得到答案.
解答 解:∵指数函数y=(a-1)x与$y={(\frac{1}{a})^x}$具有不同的单调性,
∴$\left\{\begin{array}{l}a-1>1\\ 0<\frac{1}{a}<1\end{array}\right.$,或$\left\{\begin{array}{l}\frac{1}{a}>1\\ 0<a-1<1\end{array}\right.$,
解得:a>2,
则m=${(a-1)^{\frac{1}{3}}}$>${(2-1)}^{\frac{1}{3}}$=1,
n=${(\frac{1}{a})^3}$<${(\frac{1}{2})}^{3}$<$\frac{1}{8}$,
故m>n.
点评 本题考查的知识点是指数函数的图象和性质,幂函数的图象和性质,难度中档.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
6.设x>0,函数f(x)=x•3x-318的零点,x0∈(k,k+1)(k∈N*),则k=( )
| A. | 13 | B. | 14 | C. | 15 | D. | 16 |
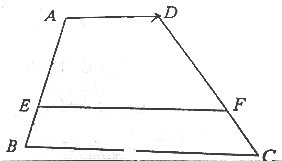 如图,已知:梯形ABCD中,AD∥EF∥BC,AE=2BE,AD=2,BC=5,设$\overrightarrow{AD}$=$\overrightarrow{a}$,用$\overrightarrow{a}$表示$\overrightarrow{EF}$,$\overrightarrow{CB}$.
如图,已知:梯形ABCD中,AD∥EF∥BC,AE=2BE,AD=2,BC=5,设$\overrightarrow{AD}$=$\overrightarrow{a}$,用$\overrightarrow{a}$表示$\overrightarrow{EF}$,$\overrightarrow{CB}$.