题目内容
9．已知函数f（x）=$\left\{\begin{array}{l}{{e}^{x}-2m+1，x≤0}\\{3x-4，x＞0}\end{array}\right.$，（m∈R），若函数f（x）在R上有且仅有两个零点，求实数m的取值范围．分析 分x＞0与x≤0讨论，从而确定方程的解的个数，即函数的零点的个数即可．
解答 解：∵当x＞0时，由3x-4=0解得x=$\frac{4}{3}$，
∴当x≤0时，方程ex-2m+1=0有且仅有一个解，
而m=$\frac{{e}^{x}+1}{2}$在[0，+∞）上是增函数，
故m≥$\frac{{e}^{0}+1}{2}$=1，
故实数m的取值范围为[1，+∞）．
点评 本题考查了分段函数的应用及函数与方程的关系应用．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
19．若函数f（x）=$\left\{\begin{array}{l}{{a}^{x}，x＞1}\\{（4-\frac{a}{2}）x+2，x≤1}\end{array}\right.$在x∈（-∞，+∞）上单调递增，则实数a的取值范围是（ ）
| A． | [2，3] | B． | （1，8） | C． | （1，5] | D． | [4，8） |
17．已知F1、F2是双曲线$\frac{{x}^{2}}{{a}^{2}}$$-\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0）的左、右焦点，过左焦点F1作直线l与双曲线的左支交于M，N两点，若|MF2|=|MN|，且MF2⊥MN，则双曲线的离心率为 （ ）
| A． | $\sqrt{5-2\sqrt{3}}$ | B． | $\sqrt{5-2\sqrt{2}}$ | C． | $\sqrt{4-2\sqrt{2}}$ | D． | $\sqrt{3-\sqrt{3}}$ |
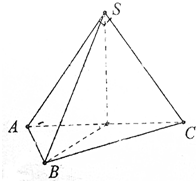在三棱锥S-ABC中，∠ASB=∠BSC=60°，∠ASC=90°，且SA=SB=SC，求证：平面ASC⊥平面ABC．
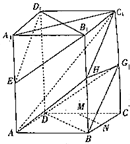如图，在平行六面体ABCD-A1B1C1D1中，E，M，N，G分别是AA1，CD，CB，CC1的中点．