题目内容
10.由三条直线x=0,x+y-2=0,x-y-2=0围成一个封闭的平面图形,则该平面图形的面积是4,若将此平面图形绕y轴旋转一周所得旋转体的表面积是8$\sqrt{2}π$.分析 画出这三条直线围成的图形,根据图形求出它的面积,
再得出旋转体是两个同底等高的圆锥组合体,求出它的表面积.
解答 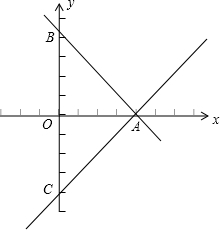 解:三条直线x=0,x+y-2=0,x-y-2=0围成一个封闭图形是等腰△ABC,如图所示;
解:三条直线x=0,x+y-2=0,x-y-2=0围成一个封闭图形是等腰△ABC,如图所示;
该△ABC的面积是$\frac{1}{2}$BC•OA=$\frac{1}{2}$×4×2=4,
将此△ABC绕y轴旋转一周,得到两个同底等高的圆锥的组合体,
该旋转体的表面积是2×π•OA•AB=2×π×2×$\sqrt{{2}^{2}{+2}^{2}}$=8$\sqrt{2}$π.
故答案为:4,8$\sqrt{2}$π.
点评 本题考查了直线方程的应用问题,也考查了旋转体的表面积的计算问题,是基础题目.

练习册系列答案
 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案
相关题目
1.圆锥SO的侧面展开图为如图所示的半径为4的半圆,半圆中∠ASC=45°.
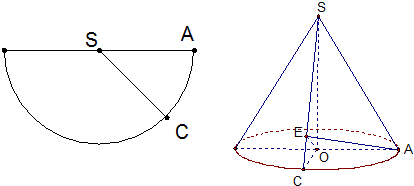
①圆锥SO的体积;
②在圆锥母线SC上是否存在一点E,使得SC⊥平面OEA,若存在,求此时SE~EC的值;若不存在,说明理由.

①圆锥SO的体积;
②在圆锥母线SC上是否存在一点E,使得SC⊥平面OEA,若存在,求此时SE~EC的值;若不存在,说明理由.
15.设α、β是两个不同的平面,l、m为两条不同的直线,命题p:若α∥β,l?α,m?β,则l∥m,命题q:l∥α,m⊥l,m?β,则α⊥β则下列命题为真命题的是( )
| A. | p∨q | B. | p∧q | C. | (¬p)∨q | D. | p∧(¬q) |
2.已知A(1,2,1),B(-1,3,4),C(1,1,1),$\overrightarrow{AP}$=2$\overrightarrow{PB}$,则$\overrightarrow{PC}$=( )
| A. | (-$\frac{1}{3}$,$\frac{8}{3}$,3) | B. | ($\frac{1}{3}$,-$\frac{8}{3}$,-3) | C. | (-$\frac{4}{3}$,$\frac{5}{3}$,2) | D. | ($\frac{4}{3}$,-$\frac{5}{3}$,-2) |
19.过点P(4,-1)且与直线3x-4y+6=0垂直的直线方程是( )
| A. | 4x-3y-19=0 | B. | 4x+3y-13=0 | C. | 3x-4y-16=0 | D. | 3x+4y-8=0 |