题目内容
2.已知A(1,2,1),B(-1,3,4),C(1,1,1),$\overrightarrow{AP}$=2$\overrightarrow{PB}$,则$\overrightarrow{PC}$=( )| A. | (-$\frac{1}{3}$,$\frac{8}{3}$,3) | B. | ($\frac{1}{3}$,-$\frac{8}{3}$,-3) | C. | (-$\frac{4}{3}$,$\frac{5}{3}$,2) | D. | ($\frac{4}{3}$,-$\frac{5}{3}$,-2) |
分析 利用向量的坐标运算即可得出.
解答 解:∵$\overrightarrow{AP}$=2$\overrightarrow{PB}$,∴$\overrightarrow{OP}-\overrightarrow{OA}=2(\overrightarrow{OB}-\overrightarrow{OP})$,
化为$\overrightarrow{OP}$=$\frac{1}{3}\overrightarrow{OA}+\frac{2}{3}\overrightarrow{OB}$=$\frac{1}{3}$(1,2,1)$+\frac{2}{3}$(-1,3,4)=$(-\frac{1}{3},\frac{8}{3},3)$,
∴$\overrightarrow{PC}$=$\overrightarrow{OC}-\overrightarrow{OP}$=$(\frac{4}{3},-\frac{5}{3},-2)$.
故选:D.
点评 本题考查了向量的坐标运算,属于基础题.

练习册系列答案
相关题目
14.在一张纸上画一个圆,圆心O,并在圆外设一点F,折叠纸圆上某点落于F点,设该点为M,抹平纸片,折痕AB,连接MO(或者OM)并延长交于AB于P,则P点轨迹为( )
| A. | 椭圆 | B. | 双曲线 | C. | 抛物线 | D. | 直线 |
12.在△ABC中,内角A,B,C所对的边分别为a,b,c,已知sinA-sinB=$\frac{1}{3}$sinC,3b=2a,2≤a2+ac≤18,设△ABC的面积为S,p=$\sqrt{2}$a-S,则p的最小值是( )
| A. | $\frac{5\sqrt{2}}{9}$ | B. | $\frac{7\sqrt{2}}{9}$ | C. | $\sqrt{2}$ | D. | $\frac{9\sqrt{2}}{8}$ |
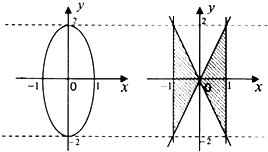 我国齐梁时代的数学家祖恒(公元前5-6世纪)提出了一条原理:“幂势既同,则买家不容异”这句话的意思是:夹在两个平行平面间的两个几何体,被平行于平面的任何平面所截.如果截得的两个截面的面积总是相等,那么这两个几何体的体积相等,设由椭圆x${\;}^{2}+\frac{{y}^{2}}{4}=1$所围成的平面图形绕y轴旋转一周得到的几何体(成为椭球体)体积为V1:由直线y=±2x,x=±1所围成的平面图形(如图阴影部分)绕y轴旋转一周所得到的几何体条件为V2:根据祖恒原理等知识,通过考察V2可得到V1的体积为$\frac{8}{3}π$.
我国齐梁时代的数学家祖恒(公元前5-6世纪)提出了一条原理:“幂势既同,则买家不容异”这句话的意思是:夹在两个平行平面间的两个几何体,被平行于平面的任何平面所截.如果截得的两个截面的面积总是相等,那么这两个几何体的体积相等,设由椭圆x${\;}^{2}+\frac{{y}^{2}}{4}=1$所围成的平面图形绕y轴旋转一周得到的几何体(成为椭球体)体积为V1:由直线y=±2x,x=±1所围成的平面图形(如图阴影部分)绕y轴旋转一周所得到的几何体条件为V2:根据祖恒原理等知识,通过考察V2可得到V1的体积为$\frac{8}{3}π$.