题目内容
(本题满分12分)已知数列 的各项均为正实数,且其前
的各项均为正实数,且其前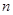 项和
项和 满足
满足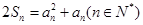 。(1)证明:数列
。(1)证明:数列 是等差数列;
是等差数列;
(2)设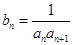 ,求数列
,求数列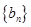 的前
的前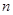 项和
项和 。
。
(1)见解析。(2)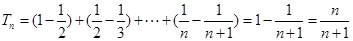 。
。
解析试题分析:(1)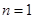 时,由
时,由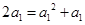 得
得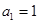 (1分)。当
(1分)。当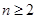 时,由
时,由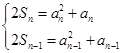 (2分)
(2分)
两式相减得: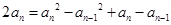 (3分),整理得:
(3分),整理得: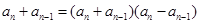 (4分)。因
(4分)。因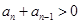 ,故
,故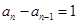 (5分)。于是数列
(5分)。于是数列 是首项
是首项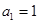 、公差
、公差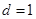 的等差数列(6分)。
的等差数列(6分)。
(2)由(1)可知: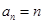 (7分),故
(7分),故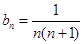 (8分)
(8分)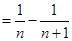 (9分),
(9分),
于是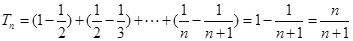 (12分)。
(12分)。
考点:本题考查 和
和 的关系、等差数列的定义、裂项相消法求和。
的关系、等差数列的定义、裂项相消法求和。
点评:数列中 与
与 的关系问题,注意不要忽视n=1是否使“通项公式”成立的检验工作。裂项相消法求和,是高考考查的重点,这是一道易错题。
的关系问题,注意不要忽视n=1是否使“通项公式”成立的检验工作。裂项相消法求和,是高考考查的重点,这是一道易错题。

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
设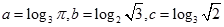 ,则( )
,则( )
A. | B.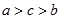 | C.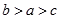 | D. |
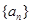 满足:
满足: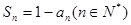 ,其中
,其中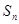 为
为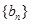 满足
满足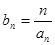 ,求
,求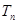 .
.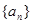 满足条件:
满足条件: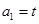 ,
,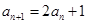
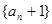 是否为等比数列;
是否为等比数列; 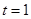 ,令
,令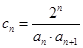 , 记
, 记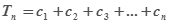
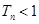
 的前
的前 项和为
项和为 ,对一切正整数,点
,对一切正整数,点 都在函数
都在函数 的图像上.
的图像上. ,求数列
,求数列 的前项和
的前项和 .
.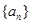 中,
中,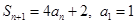 ;
;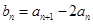 ,求证数列
,求证数列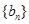 是等比数列;
是等比数列; ,求证:数列
,求证:数列 是等差数列;
是等差数列; 中,
中, .
. 的顺序,使它成为等比数列
的顺序,使它成为等比数列 的前三项,求
的前三项,求 项和.
项和. 的前四项和为10,且
的前四项和为10,且 成等比数列
成等比数列
 ,求数列
,求数列 的前
的前 项和
项和
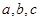 是三个连续的自然数,且成等差数列,
是三个连续的自然数,且成等差数列, 成等比数列,求
成等比数列,求