题目内容
(本题满分12分)已知等差数列 中,
中, .
.
(Ⅰ)求 的通项公式;
的通项公式;
(Ⅱ)调整数列 的前三项
的前三项 的顺序,使它成为等比数列
的顺序,使它成为等比数列 的前三项,求
的前三项,求 的前
的前 项和.
项和.
(Ⅰ)an=3n-5.
(Ⅱ)(i)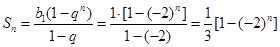 .
.
(ii) 。
。
解析试题分析:(1)先利用已知条件求得a1=-2,a8=19进而求出公差即可求{an}的通项公式;
(2)先求出数列{an}的前三项再利用等比数列满足的条件进行调整,求出等比数列{bn}的前三项,知道首项和公比,再代入等比数列的求和公式即可求出{bn}的前n项和.
解:(Ⅰ)由已知,得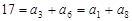 ----- -----------1分
----- -----------1分
又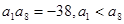 ,∴
,∴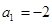 ,
,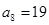 ,∴
,∴ 的公差d=3 -----3分
的公差d=3 -----3分
∴an=a1+(n-1)d=-2+3(n-1)=3n-5. ---------------------------6分
(Ⅱ)由(Ⅰ),得a1=-2,a2=1,a3=4.
依题意可得:数列{bn}的前三项为b1=1,b2=-2,b3=4或b1==4,b2=-2,b3="1" --8分
(i)当等比数列{bn}的前三项为b1=1,b2=-2,b3=4时,则q=-2 .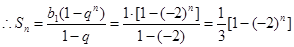 . -------------------------9分
. -------------------------9分
(ii)当第比数列{bn}的前三项为b1=4,b2=-2,b3=1时,则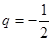 .
. -------------------12分考点:本试题主要考查了对等差数列和等比数列的性质以及数列求和公式的综合考查.
-------------------12分考点:本试题主要考查了对等差数列和等比数列的性质以及数列求和公式的综合考查.
点评:解决该试题的关键是在对等比数列进行求和时,一定要先看等比数列的公比是否为1,再代入求和公式。

练习册系列答案
相关题目
如果 ,则下列各式正确的是( )
,则下列各式正确的是( )
A.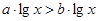 | B.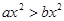 | C.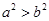 | D.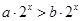 |
 的前n项和
的前n项和 ,且
,且 是
是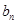 与1的等差中项。
与1的等差中项。 的通项公式;
的通项公式; ,求
,求
 ,是否存在
,是否存在 ,使得
,使得 并说明理由。
并说明理由。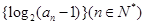 为等差数列,且
为等差数列,且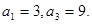
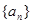 的通项公式;
的通项公式;
 的前n项和为
的前n项和为 ,且满足
,且满足 ,
, ,
, ,数列
,数列 为等比数列,求实数
为等比数列,求实数 的值;
的值; ,求数列
,求数列 的通项公式;
的通项公式; ,求数列
,求数列 的前n项和
的前n项和 .
. 的各项均为正实数,且其前
的各项均为正实数,且其前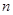 项和
项和 满足
满足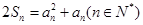 。(1)证明:数列
。(1)证明:数列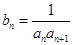 ,求数列
,求数列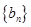 的前
的前 。
。 前
前 项和
项和 .数列
.数列 满足
满足
 ,数列
,数列 满足
满足 。(1)求数列
。(1)求数列 的通项公式;(2)求数列
的通项公式;(2)求数列 ;(3)若
;(3)若 对一切正整数
对一切正整数 的取值范围。
的取值范围。
 ,数列
,数列 满足:
满足: ,
,
 N*
N* .
. ,数列
,数列 满足:
满足: ,
, N*),
N*),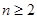 的正整数,都满足:
的正整数,都满足: .
.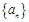 满足条件:
满足条件: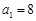 ,
,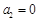 ,
,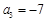 ,且数列
,且数列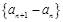
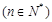 是等差数列.
是等差数列.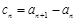 ,求数列
,求数列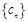 的通项公式;
的通项公式;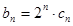 , 求
, 求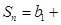
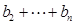 ;
;