题目内容
(本小题满分12分)
已知数列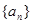 满足条件:
满足条件: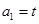 ,
,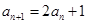
(1)判断数列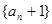 是否为等比数列;
是否为等比数列;
(2)若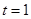 ,令
,令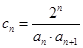 , 记
, 记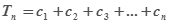
证明: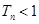
(1)当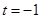 时,
时, 不是等比数列
不是等比数列
当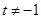 时,
时, 是以
是以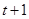 为首项,2为公比的等比数列.
为首项,2为公比的等比数列.
(2)由⑴知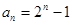 ,所以
,所以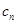
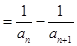
推出
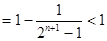
解析试题分析:(1)证明:由题意得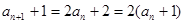 ……………2分
……………2分
又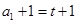 , 所以,当
, 所以,当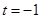 时,
时, 不是等比数列
不是等比数列
当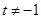 时,
时, 是以
是以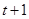 为首项,2为公比的等比数列. …………5分
为首项,2为公比的等比数列. …………5分
(2)解:由⑴知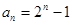 , ……………7分
, ……………7分
故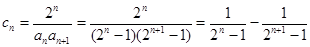
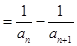 ……………9分
……………9分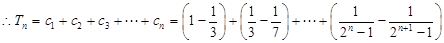
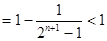 …………12分
…………12分
考点:本题主要考查递推公式,等比数列的通项公式,数列的求和。
点评:典型题,利用递推公式,求得数列的通项公式,进一步求和,“裂项相消法”是经常考查的数列求和方法。

练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
在各项均为实数的等比数列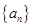 中,
中,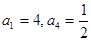 ,则
,则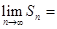 ( )
( )
| A.2 | B. 8 | C.16 | D.32 |
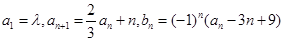 ,其中λ为实数,n为正整数.
,其中λ为实数,n为正整数.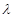 的值;
的值;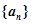 满足
满足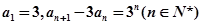 ,数列
,数列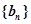 满足
满足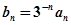 .
.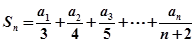 ,求满足不等式
,求满足不等式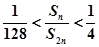 的所有正整数
的所有正整数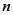 的值.
的值.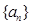 的前
的前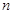 项和为
项和为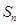 ,公差d
,公差d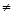 0,
0,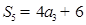 ,且
,且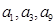 成等比数列.
成等比数列.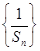 的前
的前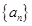 前
前 项和为
项和为 ,
,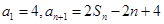 .
. 为等比数列;
为等比数列;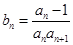 ,数列
,数列 前
前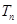 ,求证:
,求证: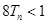 .
.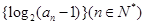 为等差数列,且
为等差数列,且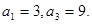
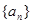 的通项公式;
的通项公式;
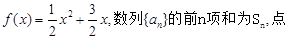
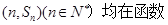
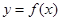
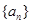 的通项公式
的通项公式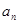 ;
; 求数列
求数列
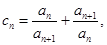 证明:
证明: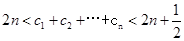 。
。 的各项均为正实数,且其前
的各项均为正实数,且其前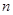 项和
项和 满足
满足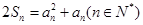 。(1)证明:数列
。(1)证明:数列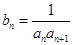 ,求数列
,求数列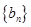 的前
的前 。
。