题目内容
(本小题满分12分)在数列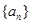 中,
中,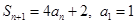 ;
;
(1)设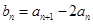 ,求证数列
,求证数列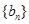 是等比数列;
是等比数列;
(2)设 ,求证:数列
,求证:数列 是等差数列;
是等差数列;
(3)求数列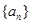 的通项公式及前n项和的公式。
的通项公式及前n项和的公式。
(1)见解析;(2)见解析;(3)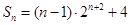 。
。
解析试题分析:(1)因为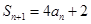 ,那么类推得到
,那么类推得到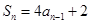 ,两式作差得到关系式,进而求解其bn
,两式作差得到关系式,进而求解其bn
(2)∵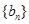 是等比数列,且首项为4,公比为2,所以
是等比数列,且首项为4,公比为2,所以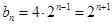 整体的思想作差来判定是否为等差数列。
整体的思想作差来判定是否为等差数列。
(3)在前两问的基础上得到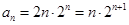 ,然后运用错位相减法得到求和。
,然后运用错位相减法得到求和。
(1)∵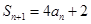 …①,∴
…①,∴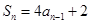 …②,②-①得
…②,②-①得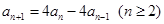 ,
,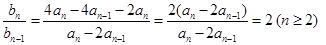 ,又
,又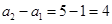 ≠0,
≠0,
∴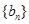 是等比数列。
是等比数列。
(2)∵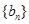 是等比数列,且首项为4,公比为2,所以
是等比数列,且首项为4,公比为2,所以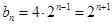
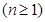 ;
;
∴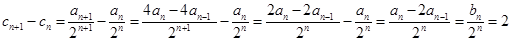 ,
,
∴数列 是等差数列;
是等差数列;
(3)∵ 是等差数列,∴
是等差数列,∴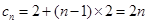 ,∴
,∴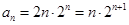
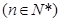 ,
,
∴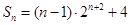 。
。
考点:本题主要考查数列的递推公式在数列的通项公式的求解中的应用,等差数列的通项公式的求解及错位相减求和方法的应用.
点评:解决该试题的关键是能根据已知的前n项和与其通项公式的关系式,得到其通项公式的结论,同时能准确的运用错位相减法求和的运用。

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
若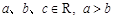 ,则下列不等式成立的是( ).
,则下列不等式成立的是( ).
A.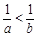 | B.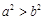 |
C.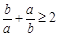 | D.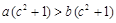 |
 的前
的前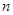 项和为
项和为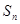 ,对一切正整数
,对一切正整数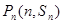 都在函数
都在函数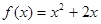 的图像上.
的图像上.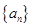 的通项公式;
的通项公式; ,求数列
,求数列 的通项公式.
的通项公式.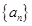 前
前 项和为
项和为 ,
,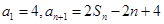 .
. 为等比数列;
为等比数列;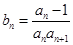 ,数列
,数列 前
前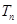 ,求证:
,求证: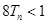 .
.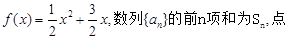
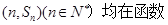
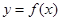
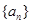 的通项公式
的通项公式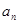 ;
; 求数列
求数列
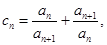 证明:
证明: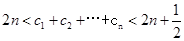 。
。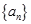 的前n项和为
的前n项和为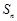 ,且满足
,且满足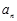 ,
,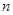 =1,2,3,….
=1,2,3,….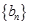 满足
满足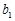 =1,且
=1,且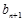 =
=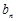 +
+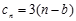 ,求数列
,求数列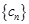 的前
的前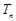 .
. 的各项均为正实数,且其前
的各项均为正实数,且其前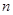 项和
项和 满足
满足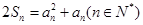 。(1)证明:数列
。(1)证明:数列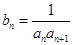 ,求数列
,求数列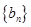 的前
的前 。
。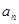 }中,
}中,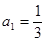 ,并且对任意
,并且对任意 都有
都有 成立,令
成立,令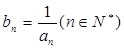 .
. }的通项公式;
}的通项公式;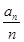 }的前n项和为
}的前n项和为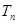 ,证明:
,证明:
 中,
中,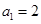 ,
,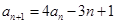 ,
,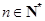 .
.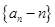 是等比数列;
是等比数列;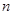 项和
项和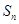 ;
;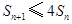 ,对任意
,对任意