äãá¢áÖàï
Àƒäãá¢À¢¡½°—üôêÅùçñ´È¤
Âì¥₤¤üA={xÀòZ|x=2kˋ1ȘkÀòZ}ÆŠ¥₤¤üB={xÀòz|x=2k+3ȘkÀòZ}òúüÁçà¥₤¤üÈ£
ÂÖඤ₤ò»fÈ´xÈˋçáÑ´ØÍÆ·öˆ[0Ș2]Ș巤₤ò»fÈ´2xÈˋçáÑ´ØÍÆ·öˆ[0Ș4]È£
Âܤ₤ò»y= ![]() çáçËç¼¥¾ú½¥ðòúÈ´ˋÀßȘ0ÈˋÀàÈ´0Ș+ÀßÈˋÈ£
çáçËç¼¥¾ú½¥ðòúÈ´ˋÀßȘ0ÈˋÀàÈ´0Ș+ÀßÈˋÈ£
ÂÉý£ÇÌåÖòçò»mȘò¿fÈ´xÈˋ=x2+mx+1öˆó̤₤ò»È£
Âïà¶fÈ´x+yÈˋ=fÈ´xÈˋfÈ´yÈˋȘúØfÈ´1Èˋ=2È˜å· ![]() +
+ ![]() +ÀÙ+
+ÀÙ+ ![]() =2016ÈÛ
=2016ÈÛ
óðøÅí»àñùçñ´çáÅ·¤éòúÈ´ Èˋ
A.ÂìÂÖÂÜ
B.ÂÖÂÜÂÉ
C.ÂìÂÜÂï
D.ÂìÂÉÂï
ÀƒÇÞ¯¡À¢D
Àƒ§ãö—À¢§ãȤÂì¥₤¤üA={xÀòZ|x=2kˋ1ȘkÀòZ}ÆŠ¥₤¤üB={xÀòz|x=2k+3ȘkÀòZ}ƒªÝÚòƒóÌò»¥₤ȘòúüÁçà¥₤¤üȘ¿òí»àñÈ£
ÂÖඤ₤ò»fÈ´xÈˋçáÑ´ØÍÆ·öˆ[0Ș2]Ș巤₤ò»fÈ´2xÈˋçáÑ´ØÍÆ·öˆ[0Ș1]Ș¿òÇÚöµÈ£
Âܤ₤ò»y= ![]() çáçËç¼¥¾ú½¥ðòúÈ´ˋÀßȘ0Èˋ¤ëÈ´0Ș+ÀßÈˋȘ¿òÇÚöµÈ£
çáçËç¼¥¾ú½¥ðòúÈ´ˋÀßȘ0Èˋ¤ëÈ´0Ș+ÀßÈˋȘ¿òÇÚöµÈ£
ÂÉçÝm=0òÝȘfÈ´xÈˋöˆé¥¤₤ò»È£çÝmÀì0òÝȘfÈ´xÈˋöˆñúóÌñú饤₤ò»È£
¿òý£ÇÌåÖòçò»mȘò¿fÈ´xÈˋöˆó̤₤ò»È˜¿òí»àñÈ£
Âïà¶fÈ´x+yÈˋ=fÈ´xÈˋfÈ´yÈˋȘúØfÈ´1Èˋ=2È˜å· ![]() =fÈ´1Èˋ=2Ș
=fÈ´1Èˋ=2Ș![]() +
+ ![]() +ÀÙ+
+ÀÙ+ ![]() =2016ÈÛ¿òí»àñÈ£
=2016ÈÛ¿òí»àñÈ£
¿òîÀȤD
Àƒ¢¥çЃ¨ö—À¢Ýƒäãø¼Øˆ¢¥ýÕêùû■äãçáíÌ¥ìéÅÑüÆŠÆÎÆûçáüÁ¿ÄøˆòÑçÐȘÅÒ؈íóöíꧡ—û■äã£ËöˆáÌñþû■äãȘù■ûúÆÅüÁë˜çáíÌ¥ìÅåȣꧡ—û■äãöˆ£ËáÌû■ä㣷£Ëñþû■äãȘù■ûúçáíÌ¥ìÅåû£ÆÅ¿ÄüçýéáÉí»àñ§ãÇÞÇùäãÈÛ

Àƒäãá¢À¢àÓÝÚøÅ¡½°—êù2011áõÀ¨2015áõá°òÅ¢šçïØçöþæÉê¢çáë°¥óò»ƒïÈ´çËö£È¤¯ìë·¥±Èˋ
áõñï | 2011 | 2012 | 2013 | 2014 | 2015 |
áõñïǺôŠ | 1 | 2 | 3 | 4 | 5 |
¢šçïØçöþæÉê¢ | 34 | 55 | 71 | 85 | 105 |
È´1ÈˋåÖë¥øÅ£Ù°—ùª¡½ò»ƒïçáíÜüÔë¥È£ 
È´2Èˋ§´êÂØ£¡—¡ûòÅ¢šçïê¢y¿ÄÆÖáõñïǺôŠxçáüÔÅå£Ä¿ÕáÈÅëÈ£
È´3Èˋâ«ÆûÈ´2ÈˋùªçûçááÈÅëȘåÊýã¡ûòÅ2016áõçᢚçïØçöþæÉê¢ÈÛ
¡§È¤£Ä¿ÕøÝüÔñ§°äçáÅÝôò¤ë§ÄƒÁçáæŸÅÀѱ°ù¿â¥ó¿¨ò§ñøÝÞöˆÈ¤
ÅÝôòȤ 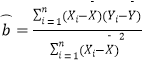 Șæï§ÄƒÁȤ
Șæï§ÄƒÁȤ ![]() ÈÛ
ÈÛ
Àƒäãá¢À¢PM2.5òúø¡¢íó½øÅø݃ÑÅÀÆÖ£·çàÆÖ2.5öÂûæçá¢éêÈöÿÈ´Øý°ó¢èàŠñö¢éêÈöÿÈˋÈÛöˆêù䧃¢°çê¼ê¢ÆŠPM2.5çáé´ÑàòúñþüÁ¿ÄȘüøýè¥₤ç§á°°úòÅøÉØ£øêøÉöÍá°Ø£òÝ¥ðÑö°çê¼ê¢ÆŠPM2.5çáò»ƒïàÓÝÚȤ
òÝ¥ð | øÉØ£ | øÉѱ | øÉà» | øÉùá | øÉöÍ |
°çê¼ê¢xÈ´ë·êƒÈˋ | 50 | 51 | 54 | 57 | 58 |
PM2.5çáé´ÑàyÈ´ö¢ù/êÂñ§ûæÈˋ | 69 | 70 | 74 | 78 | 79 |
È´1Èˋ¡ªƒïèüÝÚò»ƒïȘúŠåÖàÓë¥æ½ÝõüçøÅ£Ù°—èÂçÐë¥È£ 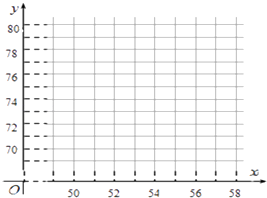
È´2Èˋ¡ªƒïèüÝÚò»ƒïȘÆûæŸÅÀѱ°ùñ´úµ°—y¿ÄÆÖxçáüÔÅå£Ä¿Õñ§°ä ![]() ȣȴÝÈê¶2ö£ÅÀò»Èˋ
ȣȴÝÈê¶2ö£ÅÀò»Èˋ
È´3Èˋà¶øÉêªë˜Ø£òÝ¥ðÑö°çê¼ê¢òú25ë·êƒÈ˜ò塪ƒïÈ´2Èˋúµ°—çáüÔÅå£Ä¿Õñ§°äåÊýãȘÇùòÝPM2.5çáé´ÑàöˆÑÁèìÈ´ÝÈê¶í«ò»ÈˋÈ¢
ýö¢¥¿¨ò§È¤ ![]() =
= 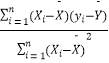 Ș
Ș ![]() =
= ![]() ˋ
ˋ ![]()
![]() ÈÛ
ÈÛ