Question

【题目】若实数满足，则称为函数的不动点．

（1）求函数的不动点；

（2）设函数，其中为实数．

① 若时，存在一个实数，使得既是的不动点，又是 的不动点（是函数的导函数），求实数的取值范围；

② 令，若存在实数，使，，， 成各项都为正数的等比数列，求证：函数存在不动点．

Answer 1

【答案】（1）函数的不动点为；（2）①，②见解析.

【解析】试题分析：

(1)结合函数的单调性可得函数的不动点为;

(2)由题意得到方程组，消去c可得实数的取值范围是，

(3)满足题意时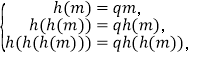结合导函数与原函数的性质讨论计算即可证得结论.

试题解析：

（1）由题意可知，．

令，．故．

列表：

x		1
		0
		极大值

所以，方程有唯一解．

所以函数的不动点为．

（2）① 由题意可知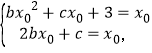

消去，得，，所以．

② ．

由题意知，，，成各项都为正数的等比数列，

故可设公比为，则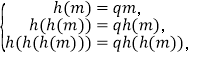

故方程有三个根，，．

又因为，所以为二次函数，

故方程为二次方程，最多有两个不等的根．则，，中至少有两个值相等．

当时，方程有实数根，也即函数存在不动点，符合题意；

当时，则，，故，又因为各项均为正数，则，也即，同上，函数存在不动点，符合题意；

当时，则，，同上，函数存在不动点，符合题意；

综上所述，函数存在不动点．