题目内容
【题目】已知数列{an}的各项都是正数，a1=1，an+12=an2+ 
（n∈N*）
（1）求证： 
≤an＜2（n≥2）
（2）求证：12（a2﹣a1）+22（a3﹣a2）+…+n2（an+1﹣an）＞ 
﹣ 
（n∈N*）
【答案】
（1）证明：∵an＞0，an+12=an2+ 
，∴an+1＞an，
∴{an}是递增数列．
由a1=1，得a2= 
，
当n≥2时，an+12﹣an2= ≥ 
，
∴an2﹣an﹣12≥ 
，an﹣12﹣an﹣22≥ 
，…，a32﹣a22≥ 
，
以上各式相加得：an2﹣a22≥ （ 
+ 
+…+ 
），
而 + +…+ ≥ 
+ 
+…+ 
=（ 
+ 
+… 
﹣ 
）= 
，
∴an2﹣2≥ 
，即an2≥2+ ，
∴an≥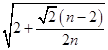 
，
又an+12=an2+ =（an+ 
）2﹣ 
＜（an+ ）2，
∴an+1＜an+ ，即an+1﹣an＜ ，
∴an﹣an﹣1＜ 
，an﹣1﹣an﹣2＜ 
，…，a3﹣a2＜ 
，a2﹣a1＜ 
，
以上各式相加得：an﹣a1＜ 
（ 
+ +…+ ）＜ （1+ 
+ +…+ 
）= （2﹣ 
）＜1，
∴an＜a1+1=2
（2）证明：∵an+12=an2+ ，
∴n2（an+12﹣an2）=an，
∴n2（an+1﹣an）= 
= ﹣ 
，
又an+1﹣an= 
＜ ，
∴n2（an+1﹣an）= ﹣ ＞ ﹣ 
﹣ 
，
∴12（a2﹣a1）+22（a3﹣a2）+…+n2（an+1﹣an）＞ 
﹣ 
（ + + +…+ 
）
＞ ﹣ （1+ + +…+ ）= ﹣ （1+1﹣ ）＞ ﹣ 
【解析】（1）由条件得an2﹣an﹣12≥ 
，an﹣12﹣an﹣22≥ 
，…，a32﹣a22≥ 
，各式累加后放缩得出结论；（2）由条件得n2（an+1﹣an）= 
= 
﹣ 
＞ ﹣ 
﹣ 
，各式累加后放缩得出结论．
【考点精析】根据题目的已知条件，利用数列的前n项和和不等式的证明的相关知识可以得到问题的答案，需要掌握数列{an}的前n项和sn与通项an的关系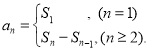
；不等式证明的几种常用方法:常用方法有：比较法（作差，作商法）、综合法、分析法；其它方法有：换元法、反证法、放缩法、构造法，函数单调性法，数学归纳法等．
