Question

【题目】有一种鱼的身体吸收汞，一定量身体中汞的含量超过其体重的1.00ppm（即百万分之一）的鱼被人食用后，就会对人体产生危害.在30条鱼的样本中发现的汞含量（单位：ppm）如下：

0.07 0.24 0.95 0.98 1.02 0.98 1.37 1.40 0.39 1.02

1.44 1.58 0.54 1.08 0.61 0.72 1.20 1.14 1.62 1.68

1.85 1.20 0.81 0.82 0.84 1.29 1.26 2.10 0.91 1.31

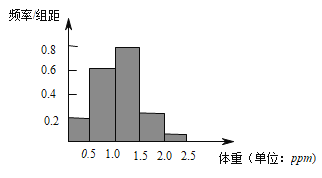
（1）请用合适的统计图描述上述数据，并分析这30条鱼的汞含量的分布特点；

（2）求出上述样本数据的平均数和标准差；

（3）从实际情况看，许多鱼的汞含量超标的原因是这些鱼在出售之前没有被检测过你认为每批这种鱼的平均承含量都比1.00ppm大吗？

（4）在上述样本中，有多少条鱼的汞含量在以平均数为中心、2倍标准差的范围内？

Answer 1

【答案】（1）73%在内；（2）平均数，样本标准差；（3）不一定；（4）28.

【解析】

（1）列出频率分布表，作出频率分布直方图；

（2）由频率分布直方图计算出样本数据的平均数和标准差的估计值；

（3）不一定能，题中数据仅仅是这一批的数据，其他批次的数据不知，这仅仅是估计值．

（4）直接确认数据在不在区间内即可．

（1）用频率分布表如下：

分组	频数	频率
	3	0.10
	10
	12	0.40
	4
	1
合计	30	1.00

作出统计图，这30条鱼的汞含量有约73%在内.

（2）样本平均数，

样本方差,

标准差..

（3）不一定，因为我们不知道其他各批鱼的汞含量分布是否都和这批鱼相同，即使其他各批鱼的汞含量分布与这批鱼相同，上面的数据也只能为这个分布作出估计，不能保证每批鱼的平均汞含量都大于1.00ppm

（4）有28条鱼的汞含量在以平均数为中心、2倍标准差的范围内.