题目内容
【题目】如图,四棱锥![]() 中,
中,![]() 为等边三角形,
为等边三角形,![]() ,平面
,平面![]() 平面
平面![]() ,点
,点![]() 为
为![]() 的中点,连接
的中点,连接![]() .
.
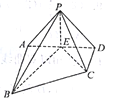
(1)求证:平面PEC![]() 平面EBC;
平面EBC;
(2)若![]() ,且二面角
,且二面角![]() 的平面角为
的平面角为![]() ,求实数
,求实数![]() 的值.
的值.
【答案】(1)见解析;(2)![]()
【解析】试题分析:(1)设![]() 为
为![]() 中点,先由等边三角形性质得
中点,先由等边三角形性质得![]() 根据面面垂直性质定理得
根据面面垂直性质定理得![]() 平面
平面![]() ,再根据面面垂直判定定理得结论,(2)先根据条件建立空间直角坐标系,设立各点坐标,利用方程组解各面法向量,由向量数量积求向量夹角,最后根据二面角与向量夹角相等或互补得方程,解得实数
,再根据面面垂直判定定理得结论,(2)先根据条件建立空间直角坐标系,设立各点坐标,利用方程组解各面法向量,由向量数量积求向量夹角,最后根据二面角与向量夹角相等或互补得方程,解得实数![]() 的值.
的值.
试题解析:(1)证明:∵![]() 为等边三角形,
为等边三角形,![]() 为
为![]() 中点,∴
中点,∴![]() ,
,
又平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
∴![]() 平面
平面![]() ,而
,而![]() 平面
平面![]() ,
,
∴平面![]() 平面
平面![]() .
.
(2)如图,在平面![]() 中,作
中,作![]() 交
交![]() 于点
于点![]() .易知
.易知![]() ,
,
以![]() 分别为
分别为![]() 轴建立空间直角坐标系.
轴建立空间直角坐标系.
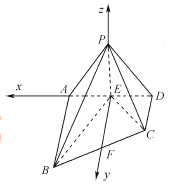
设![]() ,则
,则![]() ,
,
∴![]() ,
,
![]() ,
,
易知,平面![]() 的一个法向量
的一个法向量![]() ,
,
设平面![]() 的一个法向量为
的一个法向量为![]() ,
,
则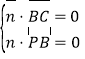 ,即
,即![]()
不妨令![]() ,解得
,解得![]() ,
,
由题知: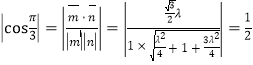 ,解得
,解得![]() .
.

练习册系列答案
 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案
相关题目
【题目】已知一组数据:
125 121 123 125 127 129 125 128 130
129 126 124 125 127 126 122 124 125
126 128
(1)填写下面的频率分布表:
分组 | 频数累计 | 频数 | 频率 |
| |||
| |||
| |||
| |||
| |||
合计 |
(2)作出频率分布直方图.
(3)根据频率分布直方图或频率分布表求这组数据的众数、中位数和平均数.
