题目内容
(本小题满分13分)
如图,已知椭圆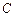 :
: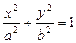
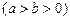 的离心率为
的离心率为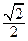 ,左焦点为
,左焦点为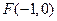 ,过点
,过点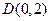 且斜率为
且斜率为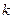 的直线
的直线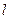 交椭圆于
交椭圆于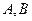 两点.
两点.
(Ⅰ)求椭圆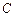 的方程;
的方程;
(Ⅱ)求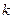 的取值范围;
的取值范围;
(Ⅲ)在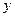 轴上,是否存在定点
轴上,是否存在定点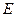 ,使
,使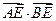 恒为定值?若存在,求出
恒为定值?若存在,求出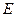 点的坐标和这个定值;若不存在,说明理由.
点的坐标和这个定值;若不存在,说明理由.
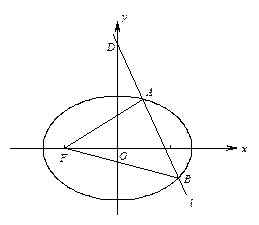
如图,已知椭圆
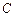 :
: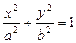
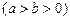 的离心率为
的离心率为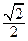 ,左焦点为
,左焦点为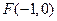 ,过点
,过点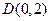 且斜率为
且斜率为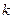 的直线
的直线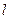 交椭圆于
交椭圆于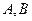 两点.
两点.(Ⅰ)求椭圆
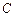 的方程;
的方程;(Ⅱ)求
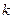 的取值范围;
的取值范围;(Ⅲ)在
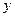 轴上,是否存在定点
轴上,是否存在定点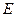 ,使
,使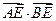 恒为定值?若存在,求出
恒为定值?若存在,求出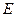 点的坐标和这个定值;若不存在,说明理由.
点的坐标和这个定值;若不存在,说明理由.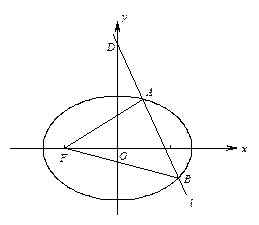
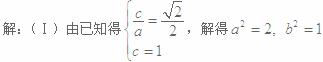

所以
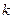 的取值范围是
的取值范围是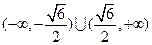 . ……6分
. ……6分(Ⅲ)设
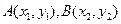 ,
,则
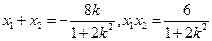 .
.又
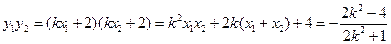 ,
,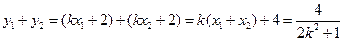 . ……7分
. ……7分设存在点
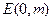 ,则
,则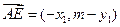 ,
,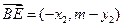 ,
,所以
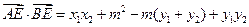
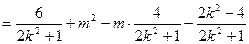
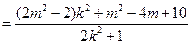 , ……9分
, ……9分要使得
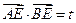 (
(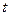 为常数),只要
为常数),只要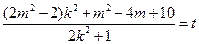 ,
,从而
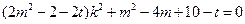 ,
,即
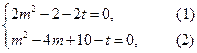 ……11分
……11分由(1)得
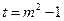 ,
,代入(2)解得
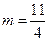 ,从而
,从而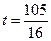 ,
, 故存在定点
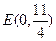 ,使
,使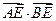 恒为定值
恒为定值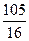 . ……13分
. ……13分略

练习册系列答案
相关题目
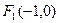 ,
,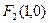 ,离心率为
,离心率为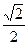 ,Q是椭圆外动点,且
,Q是椭圆外动点,且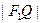 等于椭圆长轴的长,点P是线段
等于椭圆长轴的长,点P是线段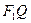 与椭圆的交点,点T是线段
与椭圆的交点,点T是线段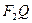 上异于
上异于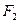 的一点,且
的一点,且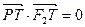 。
。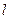 经过
经过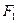 与椭圆交于M,N两点,
与椭圆交于M,N两点,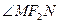 为钝角,求k的取值范围。
为钝角,求k的取值范围。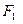 、
、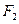 分别是椭圆
分别是椭圆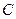 :
: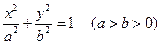 的左右焦点。
的左右焦点。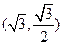 到两点
到两点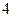 ,写出椭圆
,写出椭圆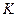 是(1)中所得椭圆上的动点,求线段
是(1)中所得椭圆上的动点,求线段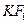 的中
的中 点
点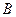 的轨迹方程;
的轨迹方程;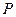 是椭圆
是椭圆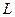 与椭圆相交于
与椭圆相交于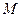 ,
,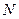 两点,当直线
两点,当直线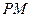 ,
,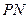 的斜率都存在,并记为
的斜率都存在,并记为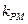 ,
,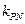 ,试探究
,试探究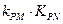 的值是否与点
的值是否与点 线
线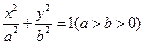 的左、右焦点分别为F1、F2,若以F2为圆心,b-c为半径作圆F2,过椭圆上一点P作此圆的切线,切点为T,且
的左、右焦点分别为F1、F2,若以F2为圆心,b-c为半径作圆F2,过椭圆上一点P作此圆的切线,切点为T,且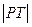 的最小值不小于
的最小值不小于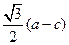 。
。 :椭圆上的点到F2的最短距离为
:椭圆上的点到F2的最短距离为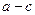 ;
; 轴的右交点为Q,过点Q作斜率为
轴的右交点为Q,过点Q作斜率为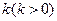 的直线
的直线 与椭圆相交于A、B两点,若OA⊥OB,求直线
与椭圆相交于A、B两点,若OA⊥OB,求直线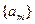 是首项为
是首项为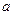 ,公差为
,公差为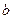 的等差数列,
的等差数列,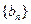 是首项为
是首项为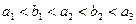 ,其中
,其中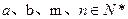 .
.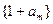 与数列
与数列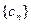 ,求数列
,求数列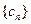 的通项公式;
的通项公式;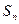 ,求证:
,求证: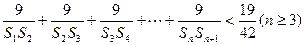 .
. 是椭圆
是椭圆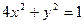 上一点,
上一点,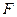 为其中一个焦点,则
为其中一个焦点,则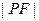 的最
的最 小值为_________.
小值为_________.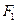 、
、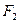 是椭圆
是椭圆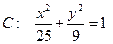 的两个焦点,
的两个焦点,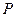 为椭圆上一点,且
为椭圆上一点,且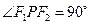 ,则
,则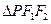 的面积 .
的面积 .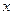 轴上的椭圆
轴上的椭圆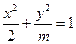 的离心率为
的离心率为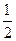 ,则
,则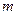 = .
= .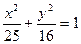 上的一点P,到椭圆一个焦点的距离为3,则P到另一焦点距离为 ( )
上的一点P,到椭圆一个焦点的距离为3,则P到另一焦点距离为 ( )