题目内容
.(本小题满分14分)
已知数列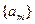 是首项为
是首项为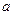 ,公差为
,公差为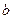 的等差数列,
的等差数列,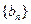 是首项为
是首项为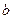 ,公比为
,公比为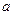 的等比数列,且满足
的等比数列,且满足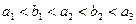 ,其中
,其中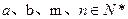 .
.
(Ⅰ)求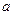 的值;
的值;
(Ⅱ)若数列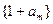 与数列
与数列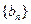 有公共项,将所有公共项按原顺序排列后构成一个新数列
有公共项,将所有公共项按原顺序排列后构成一个新数列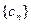 ,求数列
,求数列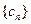 的通项公式;
的通项公式;
(Ⅲ)记(Ⅱ)中数列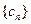 的前项之和为
的前项之和为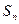 ,求证:
,求证:
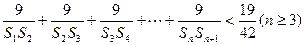 .
.
已知数列
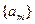 是首项为
是首项为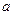 ,公差为
,公差为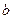 的等差数列,
的等差数列,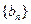 是首项为
是首项为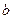 ,公比为
,公比为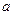 的等比数列,且满足
的等比数列,且满足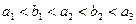 ,其中
,其中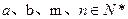 .
.(Ⅰ)求
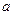 的值;
的值;(Ⅱ)若数列
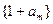 与数列
与数列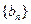 有公共项,将所有公共项按原顺序排列后构成一个新数列
有公共项,将所有公共项按原顺序排列后构成一个新数列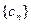 ,求数列
,求数列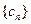 的通项公式;
的通项公式;(Ⅲ)记(Ⅱ)中数列
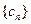 的前项之和为
的前项之和为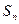 ,求证:
,求证: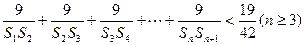 .
.解:(Ⅰ)由题设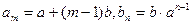 . ………1分
. ………1分
由已知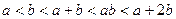 ,所以
,所以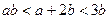 .又b>0,所以a<3. …2分
.又b>0,所以a<3. …2分
因为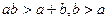 ,则
,则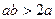 .又a>0,所以b>2,从而有
.又a>0,所以b>2,从而有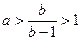 . …3分
. …3分
因为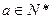 ,故
,故 . …………………4分
. …………………4分
(Ⅱ)设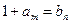 ,即
,即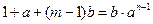 . ………………5分
. ………………5分
因为 ,则
,则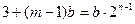 ,所以
,所以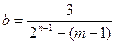 . ………………6分
. ………………6分
因为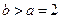 ,且b∈N*,所以
,且b∈N*,所以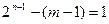 ,即
,即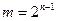 ,且b=3. ……7分
,且b=3. ……7分
故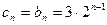 . …………………8分
. …………………8分
(Ⅲ)由题设,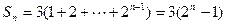 . …………………9分
. …………………9分
当
 时,
时,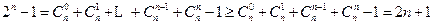 ,
,
当且仅当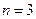 时等号成立,所以
时等号成立,所以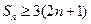 . ……………11分
. ……………11分
于是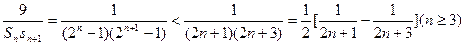 . 12分
. 12分
因为S1=3,S2=9,S3=21,则
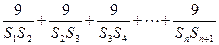
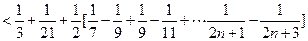
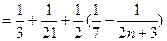
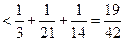 . …………………14分
. …………………14分
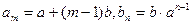 . ………1分
. ………1分由已知
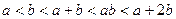 ,所以
,所以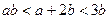 .又b>0,所以a<3. …2分
.又b>0,所以a<3. …2分因为
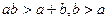 ,则
,则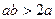 .又a>0,所以b>2,从而有
.又a>0,所以b>2,从而有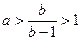 . …3分
. …3分因为
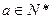 ,故
,故 . …………………4分
. …………………4分(Ⅱ)设
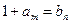 ,即
,即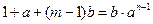 . ………………5分
. ………………5分因为
 ,则
,则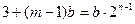 ,所以
,所以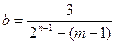 . ………………6分
. ………………6分因为
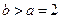 ,且b∈N*,所以
,且b∈N*,所以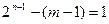 ,即
,即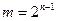 ,且b=3. ……7分
,且b=3. ……7分故
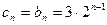 . …………………8分
. …………………8分(Ⅲ)由题设,
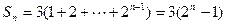 . …………………9分
. …………………9分当

 时,
时,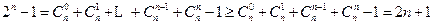 ,
,当且仅当
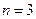 时等号成立,所以
时等号成立,所以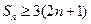 . ……………11分
. ……………11分于是
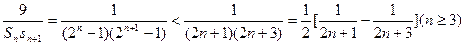 . 12分
. 12分因为S1=3,S2=9,S3=21,则
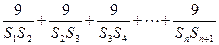
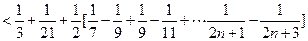
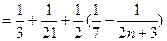
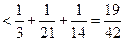 . …………………14分
. …………………14分略

练习册系列答案
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案
相关题目
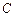 :
: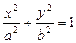
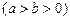 的离心率为
的离心率为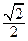 ,左焦点为
,左焦点为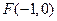 ,过点
,过点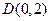 且斜率为
且斜率为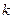 的直线
的直线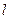 交椭圆于
交椭圆于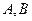 两点.
两点.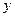 轴上,是否存在定点
轴上,是否存在定点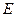 ,使
,使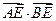 恒为定值?若存在,求出
恒为定值?若存在,求出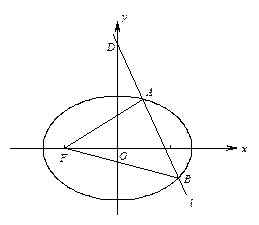
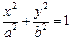
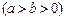 过点
过点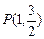 ,其左、右焦点分别为
,其左、右焦点分别为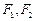 ,离心率
,离心率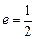 ,
,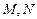 是椭圆右准线上的两个动点,且
是椭圆右准线上的两个动点,且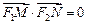 .
. 的最小值;
的最小值; 是否过定点?
是否过定点?
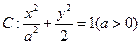 的左右焦点分别为
的左右焦点分别为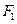 、
、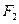 ,
,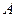 是椭圆
是椭圆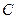 上的一点,且
上的一点,且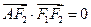 ,坐标原点
,坐标原点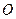 到
到 直线
直线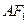 的距离为
的距离为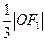 .
.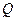 是椭圆
是椭圆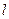 交
交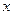 轴于点
轴于点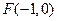 ,交
,交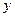 轴于点
轴于点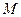 ,若
,若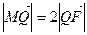 ,求直线
,求直线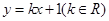 与椭圆
与椭圆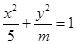 恒有公共点,则实数
恒有公共点,则实数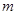 的取值范围为( )
的取值范围为( )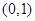
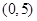
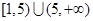
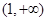
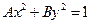 表示焦点在x轴上的椭圆,则
表示焦点在x轴上的椭圆,则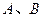 满足的条件是( )
满足的条件是( )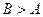
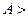
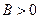
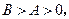
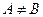 ,且
,且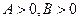
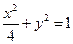 的右焦点F作直线
的右焦点F作直线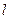 交椭圆于M,N两点,设
交椭圆于M,N两点,设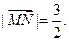
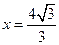 上的射影分别为M1,N1,求
上的射影分别为M1,N1,求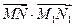 的值
的值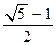 的椭圆称为“优美椭圆”.设
的椭圆称为“优美椭圆”.设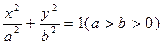 是优美椭圆,
是优美椭圆,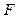 、
、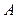 分别是它的左焦点和右顶点,B是它的短轴的一个顶点,则
分别是它的左焦点和右顶点,B是它的短轴的一个顶点,则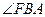 等于__________。
等于__________。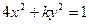 的曲线是焦点在
的曲线是焦点在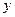 上的椭圆 ,求
上的椭圆 ,求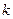 的取值范围
的取值范围