题目内容
4.已知$sin(x+\frac{π}{3})=\frac{1}{3},x∈(0,π)$,则$sin(\frac{π}{6}-x)$=-$\frac{2\sqrt{2}}{3}$;$cos(2x+\frac{π}{3})$=$\frac{7+4\sqrt{6}}{18}$.分析 由条件利用同角三角函数的基本关系、诱导公式、二倍角公式、两角差的余弦公式,求得要求式子的值.
解答 解:∵已知$sin(x+\frac{π}{3})=\frac{1}{3},x∈(0,π)$,∴x+$\frac{π}{3}$为钝角,
则$sin(\frac{π}{6}-x)$=sin[$\frac{π}{2}$-(x+$\frac{π}{3}$)]=cos(x+$\frac{π}{3}$)=-$\sqrt{{1-sin}^{2}(x+\frac{π}{3})}$=-$\frac{2\sqrt{2}}{3}$.
∴sin(2x+$\frac{2π}{3}$)=2sin(x+$\frac{π}{3}$)cos(x+$\frac{π}{3}$)=2×$\frac{1}{3}$×(-$\frac{2\sqrt{2}}{3}$)=-$\frac{4\sqrt{2}}{9}$,
cos(2x+$\frac{2π}{3}$)=2${cos}^{2}(x+\frac{π}{3})$-1=2×$\frac{8}{9}$-1=$\frac{7}{9}$,
∴$cos(2x+\frac{π}{3})$=cos[(2x+$\frac{2π}{3}$)-$\frac{π}{3}$]=cos(2x+$\frac{2π}{3}$)cos$\frac{π}{3}$+sin(2x+$\frac{2π}{3}$)sin$\frac{π}{3}$
=$\frac{7}{9}×\frac{1}{2}$+(-$\frac{4\sqrt{2}}{9}$)×$\frac{\sqrt{3}}{2}$=$\frac{7-4\sqrt{6}}{18}$,
故答案为:$\frac{7-4\sqrt{6}}{18}$.
点评 本题主要考查同角三角函数的基本关系、诱导公式、二倍角公式、两角差的余弦公式的应用,属于基础题.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案| x | … | 0.5 | 1 | 1.5 | 1.7 | 1.9 | 2 | 2.1 | 2.2 | 2.3 | 3 | 4 | 5 | 7 | … |
| y | … | 8.5 | 5 | 4.17 | 4.05 | 4.005 | 4 | 4.005 | 4.002 | 4.04 | 4.3 | 5 | 4.8 | 7.57 | … |
函数$f(x)=x+\frac{4}{x}(x>0)$在区间(0,2)上递减;
函数$f(x)=x+\frac{4}{x}(x>0)$在区间[2,+∞)上递增.
当x=2时,y最小=4
(1)用定义法证明:函数$f(x)=x+\frac{4}{x}(x>0)$在区间(0,2)递减.
(2)思考:函数$f(x)=x+\frac{4}{x}(x<0)$时,有最值吗?是最大值还是最小值?此时x为何值?(直接回答结果,不需证明)
| A. | a<c<b | B. | a<b<c | C. | b<a<c | D. | b<c<a |
| A. | (2$\sqrt{2}$,$\frac{11}{3}$) | B. | (2$\sqrt{2}$,$\frac{11}{3}$] | C. | (2$\sqrt{3}$,4) | D. | (2$\sqrt{3}$,4] |
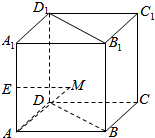 如图,在棱长为1的正方体ABCD-A1B1C1D1中,E是线段AA1的中点,M是平面BB1D1D内的点,则|AM|+|ME|的最小值是$\frac{3}{2}$;若|ME|≤1,则点M在平面BB1D1D内形成的轨迹的面积等于$\frac{π}{2}$.
如图,在棱长为1的正方体ABCD-A1B1C1D1中,E是线段AA1的中点,M是平面BB1D1D内的点,则|AM|+|ME|的最小值是$\frac{3}{2}$;若|ME|≤1,则点M在平面BB1D1D内形成的轨迹的面积等于$\frac{π}{2}$.